题目内容
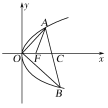
【题目】已知椭圆![]() :
:![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
(1)若点![]() 满足
满足![]() (
(![]() 为坐标原点),求弦
为坐标原点),求弦![]() 的长;
的长;
(2)若直线![]() 的斜率不为0且过点
的斜率不为0且过点![]() ,
,![]() 为点
为点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)设出![]() ,
,![]() 两点的坐标,结合关系式
两点的坐标,结合关系式![]() ,即可得线段
,即可得线段![]() 的中点坐标.利用点差法可求得直线
的中点坐标.利用点差法可求得直线![]() 的斜率,根据点斜式求得直线
的斜率,根据点斜式求得直线![]() 的方程.再结合弦长公式即可求得弦
的方程.再结合弦长公式即可求得弦![]() 的长;
的长;
(2)设出直线![]() 的方程,根据M的坐标及
的方程,根据M的坐标及![]() 可知
可知![]() .由两点的斜率公式,可得
.由两点的斜率公式,可得![]() ,将
,将![]() ,
,![]() 两点的坐标代入直线方程后,整理代入
两点的坐标代入直线方程后,整理代入![]() 的表达式,联立圆的方程,即可得关于
的表达式,联立圆的方程,即可得关于![]() 的方程.进而用韦达定理求得n的值即可.
的方程.进而用韦达定理求得n的值即可.
(1)设![]() ,
,![]()
由![]() ,且点
,且点![]() ,得
,得![]() ,
,![]() .①
.①
∴线段![]() 的中点坐标为
的中点坐标为![]() ,其在椭圆内
,其在椭圆内
由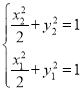 两式相减得
两式相减得![]() ,
,
整理得![]() ,即
,即![]() .
.
将①代入,得![]() .
.
∴直线![]() 方程为
方程为![]() ,即
,即![]() .
.
联立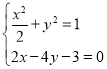 消去
消去![]() 得
得![]() ,
,
由韦达定理得![]() ,
,![]() .
.
∴![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,由题意得
,由题意得![]() ,
,
由已知![]() ,可知
,可知![]() ,
,![]() ,
,![]() 三点共线,即
三点共线,即![]() .
.
∴![]() ,即
,即![]() ,
,
解得![]() .
.
将![]() ,
,![]() ,代入得
,代入得![]() .②
.②
联立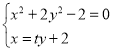 消去
消去![]() 得
得![]()
由韦达定理得![]() ,
,![]() .③
.③
将③代入②得到![]()

【题目】2019年6月,国内的![]() 运营牌照开始发放.从
运营牌照开始发放.从![]() 到
到![]() ,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对
,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对![]() 的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
用户分类 | 预计升级到 | 人数 |
早期体验用户 | 2019年8月至2019年12月 | 270人 |
中期跟随用户 | 2020年1月至2021年12月 | 530人 |
后期用户 | 2022年1月及以后 | 200人 |
我们将大学生升级![]() 时间的早晚与大学生愿意为
时间的早晚与大学生愿意为![]() 套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为
套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为![]() 套餐多支付5元的人数占所有早期体验用户的
套餐多支付5元的人数占所有早期体验用户的![]() ).
).

(1)从该地高校大学生中随机抽取1人,估计该学生愿意在2021年或2021年之前升级到![]() 的概率;
的概率;
(2)从样本的早期体验用户和中期跟随用户中各随机抽取1人,以![]() 表示这2人中愿意为升级
表示这2人中愿意为升级![]() 多支付10元或10元以上的人数,求
多支付10元或10元以上的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
![]() 套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
套餐,能否认为样本中早期体验用户的人数有变化?说明理由.