Question

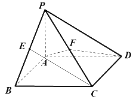
【题目】在平面直角坐标系中，椭圆（）的左右两个焦点分别是、，在椭圆上运动.

（1）若对有最大值为120°，求出、的关系式；

（2）若点是在椭圆上位于第一象限的点，过点作直线的垂线，过作直线的垂线，若直线、的交点在椭圆上，求点的坐标；

（3）若设，在（2）成立的条件下，试求出、两点间距离的函数，并求出的值域.

Answer 1

【答案】（1）；（2）；（3），的值域为．

【解析】

（1）根据椭圆定义可知，再利用余弦定理及基本不等式可得的关系式；

（2）设出点坐标，分别求出直线与直线的方程，结合在椭圆上即可求得点的坐标；

（3）把的坐标用含有的代数式表示，由两点间的距离公式可得两点间距离的函数，再换元由单调性求出其值域．

（1） 根据椭圆的定义可知，，，

因为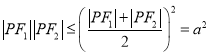

所以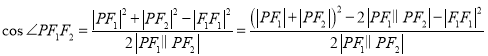

，即．

（2）设，

当时，直线斜率不存在，易知与重合，不满足题意；

当时，则直线的斜率，直线的斜率，

直线的方程，①

直线的斜率，则直线的斜率，

直线的方程，②

联立①②，解得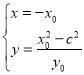：，则，

由在椭圆上，的横坐标互为相反数，纵坐标应相等，则，

，

则，又在第一象限，的坐标为；

（3）若，则，，

则，．

令，则，

，在上为增函数，

的值域为，

即的值域为．