题目内容
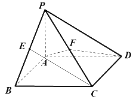
【题目】如图，在四棱锥
中，已知底面ABCD是矩形，PA⊥平面ABCD，AP=2，AB=2，AD=4，且E、F分别是PB、PC的中点。
(1)求三棱锥
的体积；
(2)求直线EC与平面PCD所成角的大小(结果用反三角函数值表示).
【答案】（1）
；（2）
【解析】
（1）利用
，转化求解即可；（2）分别以
、
、
为
轴、
轴、
轴建立空间直角坐标系，求出平面
的法向量，然后利用向量的数量积求解直线
与平面所成的角．
（1）依题意，
平面
，
.
所以三棱锥
的体积为.
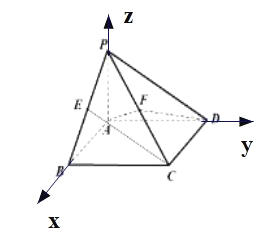
(2) 分别以、、为轴、轴、轴建立空间直角坐标系，各点坐标分别是
，
0，
，
，0，，
，4，，
，4，，
，0，
，
，0，
，
，2，，
，
由题得
,
，设平面PCD的法向量为
，
所以
所以
，
设直线与平面所成的角为
，则
，
直线与平面所成的角为．
练习册系列答案
名校课堂系列答案
相关题目
