题目内容

如图，在空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA边的中点，求证：四边形EFGH为平行四边形．

【探究】 在空间立体几何中证明某一四边形是平行四边形,首先一定要保证证明过程中证明了这个四边形是一个平面四边形,容易证明FG*DB,HEDB,从而HE∥FG,这保证了四点在同一平面内,于是我们可以应用平面几何的有关知识证明其为一平行四边形,之后可采取证明四边形一组对边平行且相等或证明四边形两组对边分别相等的方法来证明结论.

证明：∵H、E分别为AD、AB边的中点，

∴HEDB.

∵F、G分别为BC、CD边的中点，故FGDB．

∴HEFG．

故四边形EFGH为平行四边形．

练习册系列答案
相关题目
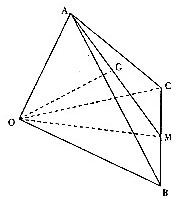精英家教网如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设
OA
=
a
，
OB
=
b
，
OC
=
c
．
（1）用基底{
a
 ， 
b
 ，
c
}表示向量
OG
；
（2）若|
a
|=|
b
|=|
c
|=
3
，且
a
与
b
、
c
夹角的余弦值均为
1
3
，
b
与
c
夹角为60°，求|
OG
|．
如图，在空间四边形ABCD中，点E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且
CF
CB
=
CG
CD
=
2
3
，则（　　）
如图，在空间四边形OABC中，已知E是线段BC的中点，G为AE的中点，若
OA
，
OB
，
OC
分别记为
a
，
b
，
c
，则用
a
，
b
，
c
表示
OG
的结果为
OG
=
1
2
a
+
1
4
b
+
1
4
c
1
2
a
+
1
4
b
+
1
4
c
．
如图，在空间四边形PABC中，PA⊥面ABC，AC⊥BC，若点A在PB、PC上的射影分别是E、F，求证：EF⊥PB.

如图，在空间四边形ABCD中，点E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且＝＝，则（　　）

（A）EF与GH互相平行

（B）EF与GH异面

（C）EF与GH的交点M可能在直线AC上，也可能不在直线AC上

（D）EF与GH的交点M一定在直线AC上

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网