题目内容
一个几何体是由圆柱![]() 和三棱锥
和三棱锥![]() 组合而成,点
组合而成,点![]() 、
、![]() 、
、![]() 在圆柱上底面圆
在圆柱上底面圆![]() 的圆周上,
的圆周上,![]() ,
,![]() ,
,![]() ,其正视图、侧视图如图所示.
,其正视图、侧视图如图所示.
⑴求证:![]() ;
;
⑵求锐二面角![]() 的大小.
的大小.
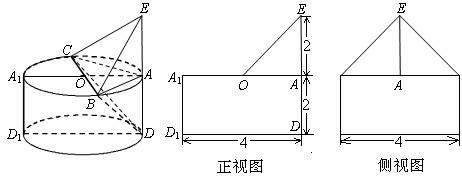 |
方法1:(1)证明:因为![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() .………………………………………5分
.………………………………………5分
(2)解: ![]() ,
,![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,
由(1)知,![]() ,
,![]() ,所
,所![]() 以
以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由(1)知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,即△
,即△![]() 为直角三角形.
为直角三角形.
在![]() △
△![]() 中,
中,![]() ,
,![]() ,则
,则![]() .
.
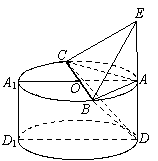 |
由![]() ,解得
,解得![]() .
.
因为![]() .
.
所以![]()
![]() .
.
所以二面角![]() 的平面角大小为
的平面角大小为![]() .
.
方法2:(2)解:设![]() 是平面
是平面![]() 的法向量,因为
的法向量,因为![]()
![]() ,
,
所以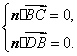 即
即![]()
![]()
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由(1)知,![]() ,又
,又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
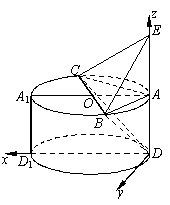
因为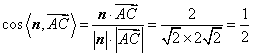 ,
,
所以![]() .
.
而![]() 等于二面角
等于二面角![]() 的平面角,
的平面角,
所以二面角![]() 的平面角大小为
的平面角大小为![]() .……………………………………12分
.……………………………………12分

练习册系列答案
相关题目













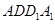 和三棱锥
和三棱锥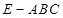 组合而成,点
组合而成,点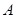 、
、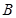 、
、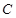 在圆
在圆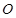 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中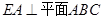 ,
,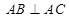 ,
,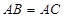 ,
,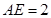 .
.
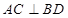 ;
;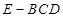 的体积.
的体积. 和三棱锥
和三棱锥 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中 ,
, ,
, ,
, .
.
 ;
; 的平面角的大小.
的平面角的大小. 和三棱锥
和三棱锥 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中 ,
, ,
, ,
, .
.
 ;
; 的平面角的大小.
的平面角的大小. (2)求三棱锥
(2)求三棱锥