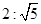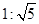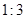题目内容
已知中心在坐标原点,焦点在 轴上的双曲线
轴上的双曲线 的渐近线方程为
的渐近线方程为 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
A. | B. | C. | D.5 |
B
解析试题分析:由题意,得 ,所以离心率
,所以离心率 =
= ,故选B.
,故选B.
考点:双曲线的几何意义.

练习册系列答案
相关题目
抛物线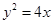 的焦点坐标为( )
的焦点坐标为( )
A.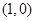 | B.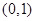 | C.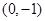 | D.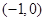 |
已知双曲线的离心率为 ,焦点是
,焦点是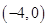 ,
,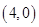 ,则双曲线方程为( )
,则双曲线方程为( )
A.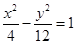 | B.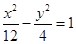 |
C. | D.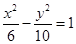 |
若双曲线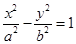 的离心率为
的离心率为 ,则其渐近线方程为( )
,则其渐近线方程为( )
| A.y=±2x | B.y=±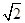 x x |
C.y=±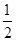 x x | D.y=±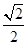 x x |
曲线y=ex在点A(0,1)处的切线斜率为( )
| A.1 | B.2 | C.e | D. |
已知F为双曲线C: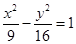 的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为( )
的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为( )
| A.11 | B.22 | C.33 | D.44 |
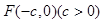 是双曲线
是双曲线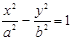 的左焦点,离心率为
的左焦点,离心率为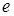 ,过
,过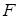 且平行于双曲线渐近线的直线与圆
且平行于双曲线渐近线的直线与圆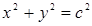 交于点
交于点 ,且点
,且点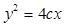 上,则
上,则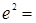 ( )
( )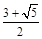
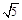
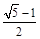
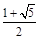
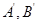 ,则
,则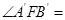 ( )
( ) B.
B.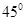 C.
C.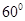 D.
D.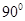
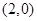 ,抛物线C:
,抛物线C: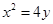 的焦点F。射线FA与抛物线C相交于点M,与其准线相交于点N,则
的焦点F。射线FA与抛物线C相交于点M,与其准线相交于点N,则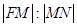 =( )
=( )