题目内容
函数f(x)的图象与函数g(x)=( )x的图象关于直线y=x对称,则f(2x-x2)的单调减区间为
)x的图象关于直线y=x对称,则f(2x-x2)的单调减区间为
- A.(-∞,1)
- B.[1,+∞]
- C.(0,1)
- D.[1,2]
C
分析:由题意知函数f(x)是函数g(x)=( )x的反函数,根据反函数的定义求出f(x)=
)x的反函数,根据反函数的定义求出f(x)= ,再由复合函数的单调性即可求出f(2x-x2)的单调减区间
,再由复合函数的单调性即可求出f(2x-x2)的单调减区间
解答:由题意函数f(x)的图象与函数g(x)=( )x的图象关于直线y=x对称知,函数f(x)是函数g(x)=(
)x的图象关于直线y=x对称知,函数f(x)是函数g(x)=( )x的反函数
)x的反函数
所以f(x)=
即f(2x-x2)=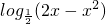
令2x-x2≥0,解得0≤x≤2,
又f(x)= 是减函数,t=2x-x2在(-∞,1)上增,在(1,+∞)上减
是减函数,t=2x-x2在(-∞,1)上增,在(1,+∞)上减
由复合函数的单调性知,f(2x-x2)的单调减区间为(0,1)
故选C
点评:本题考查复合函数的单调性及反函数的定义,解答的关键是熟练掌握反函数的定义及复合函数单调性的判断规则,本题是一个易错题,易因为忘记求函数的定义域导致误选A
分析:由题意知函数f(x)是函数g(x)=(
 )x的反函数,根据反函数的定义求出f(x)=
)x的反函数,根据反函数的定义求出f(x)= ,再由复合函数的单调性即可求出f(2x-x2)的单调减区间
,再由复合函数的单调性即可求出f(2x-x2)的单调减区间解答:由题意函数f(x)的图象与函数g(x)=(
 )x的图象关于直线y=x对称知,函数f(x)是函数g(x)=(
)x的图象关于直线y=x对称知,函数f(x)是函数g(x)=( )x的反函数
)x的反函数所以f(x)=

即f(2x-x2)=
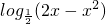
令2x-x2≥0,解得0≤x≤2,
又f(x)=
 是减函数,t=2x-x2在(-∞,1)上增,在(1,+∞)上减
是减函数,t=2x-x2在(-∞,1)上增,在(1,+∞)上减由复合函数的单调性知,f(2x-x2)的单调减区间为(0,1)
故选C
点评:本题考查复合函数的单调性及反函数的定义,解答的关键是熟练掌握反函数的定义及复合函数单调性的判断规则,本题是一个易错题,易因为忘记求函数的定义域导致误选A

练习册系列答案
相关题目