题目内容
若正项数列 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等比数列.
级等比数列.
(1)已知数列 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为 ,求
,求 的值;
的值;
(2)若 为常数),且
为常数),且 是
是 级等比数列,求
级等比数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前
的前 项和
项和 ;
;
(3)证明: 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列.
级等比数列.
(1)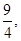 (2)
(2)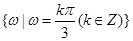 ,0,(3)详见解析.
,0,(3)详见解析.
解析试题分析:(1)解新定义数列问题,关键从定义出发,建立等量关系.  ,
,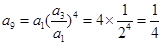 ,
,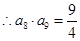 ,(2)本题化简是关键.因为
,(2)本题化简是关键.因为 是
是 级等比数列,所以
级等比数列,所以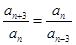
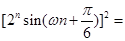
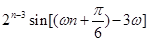
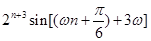

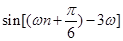
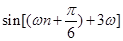
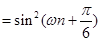
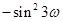
所以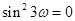 ,
,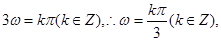
 最小正值等于
最小正值等于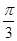 ,此时
,此时
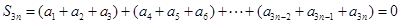 ,(3)充分性就是验证,易证,关键在于证必要性,可从两者中在交集(共同元素)出发.
,(3)充分性就是验证,易证,关键在于证必要性,可从两者中在交集(共同元素)出发. 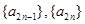 ,
,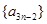 成等比数列, 因此
成等比数列, 因此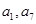 既是
既是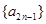 中的项,也是
中的项,也是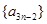 中的项,
中的项, 既是
既是 中的项,也是中
中的项,也是中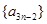 的项,可得它们公比的关系,进而推出三者结构统一,得出等比数列的结论.
的项,可得它们公比的关系,进而推出三者结构统一,得出等比数列的结论.
解(1) (2分)
(2分)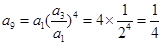
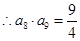 (4分)
(4分)
(2) 是
是 级等比数列,
级等比数列,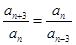
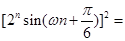
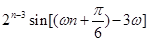
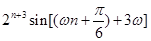 (1分)
(1分)
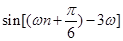
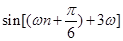
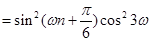
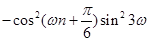
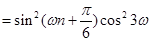
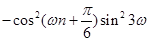
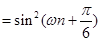
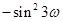
所以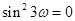 ,
,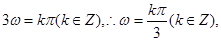
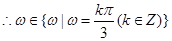 (3分)
(3分) 最小正值等于
最小正值等于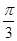 ,此时
,此时
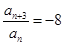 ,
,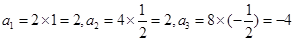 ,
,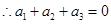
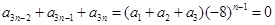 (5分)
(5分)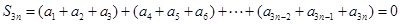 (6分)
(6分)
(3)充分性:若 为等比数列,则
为等比数列,则
对一切 成立,显然对
成立,显然对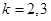 成立。
成立。
所以 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列。 (2分)
级等比数列。 (2分)
必要性:若 为
为 级等比数列,
级等比数列,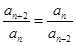 ,则
,则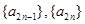 均成等比数列,设等比数列
均成等比数列,设等比数列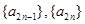 的公比分别为
的公比分别为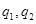 ,
, 为
为
练习册系列答案
相关题目
 ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为 级分形图.
级分形图.
 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
,
 求数列
求数列 的前
的前 项和
项和 .
.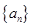 和
和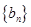 满足:
满足: ,其中
,其中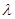 为实数,
为实数,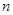 为正整数.
为正整数. 不成等比数列;
不成等比数列;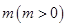 万吨.
万吨.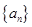 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;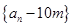 是等比数列;
是等比数列;
 满足:
满足: ,则
,则 ;
; 的前
的前 项和
项和 满足:
满足: (
( 为常数,
为常数,
 的通项公式;
的通项公式; ,若数列
,若数列 为等比数列,求
为等比数列,求