题目内容
已知椭圆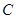 :
: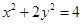 .
.
(1)求椭圆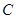 的离心率;
的离心率;
(2)设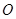 为原点,若点
为原点,若点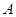 在椭圆
在椭圆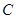 上,点
上,点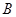 在直线
在直线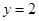 上,且
上,且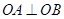 ,试判断直线
,试判断直线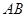 与圆
与圆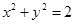 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
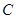 :
: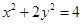 .
.(1)求椭圆
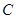 的离心率;
的离心率;(2)设
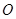 为原点,若点
为原点,若点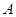 在椭圆
在椭圆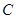 上,点
上,点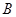 在直线
在直线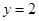 上,且
上,且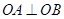 ,试判断直线
,试判断直线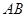 与圆
与圆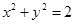 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.(1) ;(2)直线
;(2)直线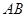 与圆
与圆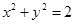 相切.
相切.
 ;(2)直线
;(2)直线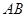 与圆
与圆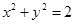 相切.
相切.试题分析:(1)把椭圆
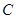 :
: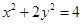 化为标准方程,确定
化为标准方程,确定 ,
, ,利用
,利用 求得离心率;(2)设点
求得离心率;(2)设点 ,
, ,其中
,其中 ,由
,由 ,即
,即 ,用
,用 、
、 表示
表示 ,当
,当 或
或 分别根据点到直线的距离公式求出圆心到直线的距离,与圆的半径比较,从而判断直线
分别根据点到直线的距离公式求出圆心到直线的距离,与圆的半径比较,从而判断直线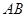 与圆
与圆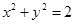 的位置关系.
的位置关系.(1)由题意椭圆
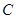 的标准方程为
的标准方程为 ,
,所以
 ,
, ,从而
,从而 ,
,所以
 .
.(2)直线
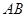 与圆
与圆 相切,证明如下:
相切,证明如下:设点
 ,
, ,其中
,其中 ,
,因为
 ,所以
,所以 ,即
,即 ,解得
,解得 ,
,当
 时,
时, ,代入椭圆
,代入椭圆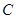 的方程得
的方程得 ,
,此时直线
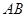 与圆
与圆 相切.
相切.当
 时,直线
时,直线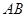 的方程为
的方程为 ,
,即
 ,
,圆心到直线
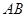 的距离为
的距离为 ,又
,又 ,
, ,
,故
 .
.故此直线
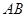 与圆
与圆 相切.
相切.
练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,,右顶点为A,上顶点为B.已知
,,右顶点为A,上顶点为B.已知 =
=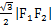 .
. ,经过点
,经过点 的直线
的直线 与该圆相切与点M,
与该圆相切与点M, =
= .求椭圆的方程.
.求椭圆的方程.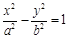 与椭圆
与椭圆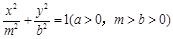 的离心率互为倒数,则( )
的离心率互为倒数,则( )



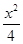 +
+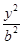 =1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )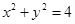 的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线
的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线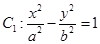 过点P且离心率为
过点P且离心率为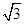 .
.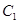 的方程;
的方程;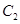 过点P且与
过点P且与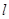 过
过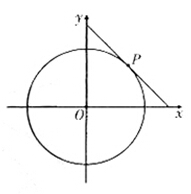
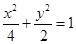 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )
的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为 ( )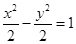



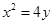 的准线与椭圆
的准线与椭圆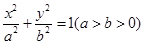 相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )
相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )



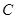 :
: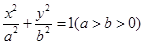 经过点
经过点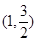 ,其离心率
,其离心率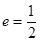 .
.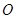 作不与坐标轴重合的直线
作不与坐标轴重合的直线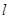 交椭圆
交椭圆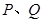 两点,过
两点,过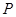 作
作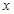 轴的垂线,垂足为
轴的垂线,垂足为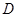 ,连接
,连接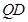 并延长交椭圆
并延长交椭圆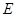 ,试判断随着
,试判断随着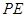 与
与 ,离心率等于
,离心率等于 ,则椭圆的方程是( )
,则椭圆的方程是( ) 


