题目内容
已知动点A、B分别在x轴、y轴上,且满足|AB|=2,点P在线段AB上,且(1)求点P的轨迹方程C;
(2)若点M、N是曲线C上关于原点对称的两个动点,点Q的坐标为(![]() ,3),求△QMN的面积S的最大值.
,3),求△QMN的面积S的最大值.
解:(1)设点A、B、P的坐标分别为(a,0)、(0,b)、(x,y),
则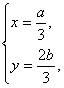 即
即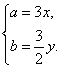 由|AB|=2,得a2+b2=4,
由|AB|=2,得a2+b2=4,
∴曲线C的方程为![]() =1.
=1.
(2)设M(x1,y1),N(-x1,-y1),则|MN|=![]() .
.
当x1≠0时,设直线MN的方程为y=![]() x,则点Q到直线MN的距离h=
x,则点Q到直线MN的距离h=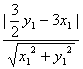 ,
,
∴△QMN的面积S=![]() ·2
·2![]() ·
·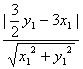 =|
=|![]() y1-3x1|.
y1-3x1|.
∴S2=|![]() y1-3x1|2=9x12+
y1-3x1|2=9x12+![]() y12-9x1y1.
y12-9x1y1.
又∵![]() =1,∴9x12+
=1,∴9x12+![]() y12=4.∴S2=4-9x1y1.
y12=4.∴S2=4-9x1y1.
而1=![]() ≥-2·
≥-2·![]() ·
·![]() =
=![]() ,
,
则-9x1y1≤4,即S2≤8,S≤2![]() .
.
当且仅当![]() =
=![]() 时,即x1=
时,即x1=![]() y1时,“=”成立.
y1时,“=”成立.
当x1=0时,|MN|=![]() ,△QMN的面积S=
,△QMN的面积S=![]() ×
×![]() ×
×![]() =2.
=2.
∴S有最大值22.

练习册系列答案
相关题目
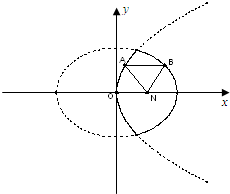 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆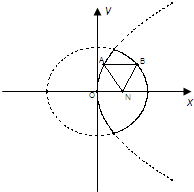 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆 及椭圆
及椭圆 的实线上运动,若
的实线上运动,若 ∥
∥ 轴,点N的坐标
轴,点N的坐标 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.