题目内容
14．在△ABC中，tanA是以-4为第4项、4为第8项的等差数列{an}的公差，tanB是以$\frac{1}{3}$为第2项、9为第5项的等比数列{bn}的公比，则△ABC是（ ）| A． | 钝角三角形 | B． | 等腰直角三角形 | C． | 锐角三角形 | D． | 以上都不对 |
分析 由题意可得tanA和tanB，进而由三角形的内角和以及两角和的正切公式可得tanC，可得三角形形状．
解答 解：由题意可得tanA=$\frac{4-（-4）}{4}$=2，tanB=$\root{3}{\frac{9}{\frac{1}{3}}}$=3，
∴tanC=-tan（A+B）=-$\frac{tanA+tanB}{1-tanAtanB}$=-$\frac{2+3}{1-2×3}$=1，
∴A、B、C均为锐角，故三角形为锐角三角形．
故选：C．
点评 本题考查等差数列和等比数列的通项公式，涉及三角形形状的判定，属基础题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
4．在区间[0，2]上随机地取一个数x，则事件“-1≤log${\;}_{\frac{1}{2}}$x≤1”发生的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
两个半径分别为r1，r2的圆M，N，公共弦AB长为3，如图所示，则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9．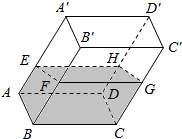
如图，在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：