题目内容
2.已知函数f(x)=log2(x+$\sqrt{{x}^{2}+1}$),且f(1-a)+f(2+b)=0,又x≥1时恒有0≤x2+ax+b≤x3-1,则a•b的值等于-2.分析 先根据y=x3-1为增函数,求出y的最小值,得到a+b+1=0,即b+2=1-a,根据f(1-a)+f(2+b)=0,得到f(1-a)=0,代入求出a的值,再求出b的值,问题得以解决.
解答 解:∵x≥1时恒有0≤x2+ax+b≤x3-1,
∴a+b+1=0,
∴b+2=1-a,
∵f(1-a)+f(2+b)=0,
∴2f(1-a)=0,
∴f(1-a)=0,
∵f(x)=log2(x+$\sqrt{{x}^{2}+1}$),
∴log2(1-a+$\sqrt{(1-a)^{2}+1}$)=0,
∴1-a+$\sqrt{(1-a)^{2}+1}$=1,
∴$\sqrt{(1-a)^{2}+1}$=a,
∴(1-a)2+1=a2,
解得a=1,
∴b=-1-a=-2,
∴a•b=-2,
故答案为:-2
点评 本题考查了函数恒成立的问题,以及对数函数的性质,以及函数值的求法,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
12.设集合A={$\frac{n}{2}$|n∈Z},B={n|n∈Z},C={n+$\frac{1}{2}$|n∈Z},D={$\frac{n}{3}$+$\frac{1}{6}$|n∈Z},则在下列关系式中,成立的是( )
| A. | A$\underset{?}{≠}$B$\underset{?}{≠}$C$\underset{?}{≠}$D | B. | A∩B=∅,C∩D=∅ | C. | A=B∪C,C$\underset{?}{≠}$D | D. | A∪B=B ,C∩D=∅ |
14.在△ABC中,tanA是以-4为第4项、4为第8项的等差数列{an}的公差,tanB是以$\frac{1}{3}$为第2项、9为第5项的等比数列{bn}的公比,则△ABC是( )
| A. | 钝角三角形 | B. | 等腰直角三角形 | C. | 锐角三角形 | D. | 以上都不对 |
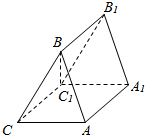 斜三棱柱ABC-A1B1C1的两底面为等腰三角形,直角边AB=AC=6,BC1⊥AC,BC1=2$\sqrt{6}$,侧棱CC1与平面ABC1成60°角.
斜三棱柱ABC-A1B1C1的两底面为等腰三角形,直角边AB=AC=6,BC1⊥AC,BC1=2$\sqrt{6}$,侧棱CC1与平面ABC1成60°角.