题目内容
(本小题满分12分)
已知抛物线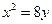 的焦点为
的焦点为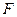 ,其准线与
,其准线与 轴交于点
轴交于点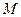 ,过
,过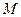 作直线与抛物线在第一象限的部分交于
作直线与抛物线在第一象限的部分交于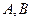 两点,其中
两点,其中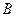 在
在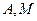 之间。直线
之间。直线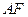 与抛物线的另一个交点为
与抛物线的另一个交点为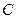 。
。
(Ⅰ)求证:点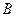 与
与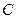 关于
关于 轴对称。
轴对称。
(Ⅱ)若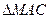 的内切圆半径
的内切圆半径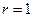 ,求
,求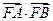 的值。
的值。
已知抛物线
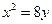 的焦点为
的焦点为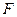 ,其准线与
,其准线与 轴交于点
轴交于点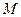 ,过
,过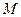 作直线与抛物线在第一象限的部分交于
作直线与抛物线在第一象限的部分交于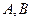 两点,其中
两点,其中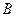 在
在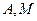 之间。直线
之间。直线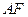 与抛物线的另一个交点为
与抛物线的另一个交点为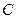 。
。(Ⅰ)求证:点
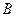 与
与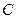 关于
关于 轴对称。
轴对称。(Ⅱ)若
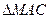 的内切圆半径
的内切圆半径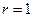 ,求
,求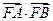 的值。
的值。(Ⅰ)F(0,2),M(0,-2)设直线AB :  ,直线AC:
,直线AC: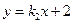
设A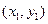 ,B
,B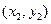 ,C
,C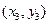 ,将
,将 代入
代入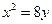 得:
得:
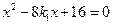 ,由
,由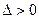
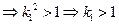
又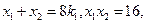 。。。① 同理:
。。。① 同理: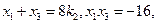 。。。②
。。。②
由①②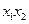 =
=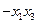 ,
,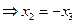
由抛物线的对称性知:点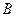 与
与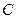 关于
关于 轴对称 6分
轴对称 6分
(Ⅱ)由1知Y轴平分角AMC,故三角形MAC的内心必在Y轴上,设为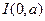 则I到边AC,AM的距离都是1,所以:
则I到边AC,AM的距离都是1,所以: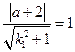 ,
,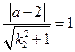 。。。③
。。。③
把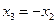 代入②:
代入②: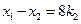 ,所以
,所以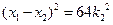 ,
,
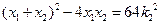 ,结合①:
,结合①:
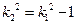 ,。。。④
,。。。④
③④联立,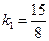
所以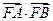 =
=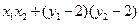 =
=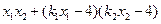
= =
=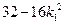 =
=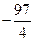 12分
12分
 ,直线AC:
,直线AC: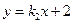
设A
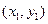 ,B
,B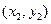 ,C
,C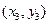 ,将
,将 代入
代入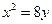 得:
得: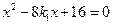 ,由
,由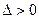
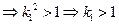
又
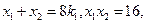 。。。① 同理:
。。。① 同理: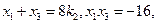 。。。②
。。。②由①②
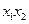 =
=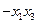 ,
,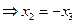
由抛物线的对称性知:点
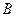 与
与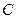 关于
关于 轴对称 6分
轴对称 6分(Ⅱ)由1知Y轴平分角AMC,故三角形MAC的内心必在Y轴上,设为
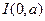 则I到边AC,AM的距离都是1,所以:
则I到边AC,AM的距离都是1,所以: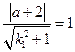 ,
,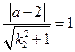 。。。③
。。。③把
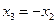 代入②:
代入②: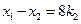 ,所以
,所以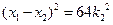 ,
,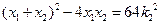 ,结合①:
,结合①:
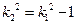 ,。。。④
,。。。④③④联立,
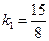
所以
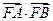 =
=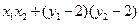 =
=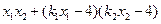
=
 =
=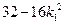 =
=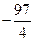 12分
12分略

练习册系列答案
相关题目
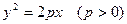 上有一点
上有一点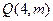 到焦点
到焦点 的距离为5,
的距离为5,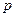 及
及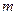 的值。
的值。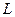 交抛物线于A,B两点,若
交抛物线于A,B两点,若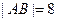 ,求直线
,求直线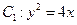 和圆
和圆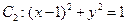 ,直线
,直线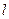 经过C1的焦点F,依次交C1,C2于A,B,C,D四点,则
经过C1的焦点F,依次交C1,C2于A,B,C,D四点,则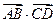 的值为( )
的值为( )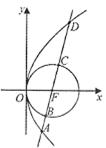
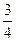
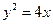 的焦点为圆心,且过坐标原点的圆的方程为
的焦点为圆心,且过坐标原点的圆的方程为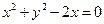

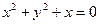

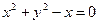
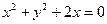
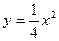 ,则准线方程为 ( )
,则准线方程为 ( )
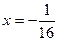
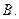
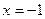
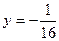
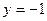
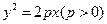 的焦点,过F且与抛物线G的对称轴垂直的直线被抛物线G截得的线段长为4.
的焦点,过F且与抛物线G的对称轴垂直的直线被抛物线G截得的线段长为4.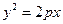 的焦点与双曲线
的焦点与双曲线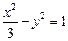 的右焦点重合,则
的右焦点重合,则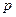 的值为( )
的值为( )