题目内容
19.已知二次函数f(x)=ax2-4x-5a,(1)当a=-3时,求不等式f(x)<0的解集;
(2)若函数f(x)图象的对称轴在区间(-$\sqrt{6}$,-2)内,求f($\frac{2}{a}$)的最小值.
分析 (1)将a的值代入,解不等式即可;(2)求出a的范围,根据级别不等式的性质求出f($\frac{2}{a}$)的最小值即可.
解答 解:(1)a=-3时:f(x)=-3x2-4x+15<0,
解得:x>$\frac{5}{3}$或x<-3,
故不等式的解集是{x|x>$\frac{5}{3}$或x<-3};
(2)f(x)的对称轴x=$\frac{2}{a}$,
∴-$\sqrt{6}$<$\frac{2}{a}$<-2,解得:-1<a<0或a<-$\frac{\sqrt{6}}{3}$,
即0<-a<1或-a>$\frac{\sqrt{6}}{3}$,
而f($\frac{2}{a}$)=-$\frac{4}{a}$-5a≥2$\sqrt{20}$=4$\sqrt{5}$,
当且仅当-$\frac{4}{a}$=-5a即a=-$\frac{2\sqrt{5}}{5}$时“=”成立.
点评 本题考查了二次函数的性质,考查解不等式以及级别不等式的性质,是一道中档题.

练习册系列答案
相关题目
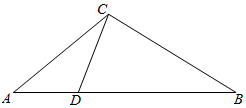 如图,在△ABC中,点D在边AB上,AC=7,CD=5,BC=$\sqrt{31}$,BD=2AD
如图,在△ABC中,点D在边AB上,AC=7,CD=5,BC=$\sqrt{31}$,BD=2AD