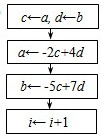
题目内容
利用数列{an}:a1,a2,a3,…,an,…构造一个新的数列:a1,(a2-a1),(a3-a2),…,(an-an-1),…此数列是首项为1,公差为2的等差数列.(1)求数列{an}的通项公式.
(2)若bn=
| 1 | ||
|
分析:(1)由累加法知an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=n+
×2=n2.
(2)bn=
=
=
-
,由此能求出T2009.
| n(n-1) |
| 2 |
(2)bn=
| 1 | ||
|
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:(1)an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=n+
×2=n2
∴an=n2
(2)bn=
=
=
-
∴T2009=1-
=
| n(n-1) |
| 2 |
∴an=n2
(2)bn=
| 1 | ||
|
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴T2009=1-
| 1 |
| 2010 |
| 2009 |
| 2010 |
点评:本题考查数列的性质和应用,解题时要注意累加法和裂项求和法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
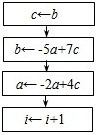
 (2013•泰安二模)已知数列an+1=an+nan中,a1=1,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )
(2013•泰安二模)已知数列an+1=an+nan中,a1=1,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )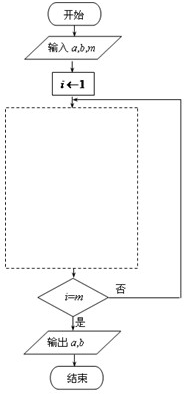 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,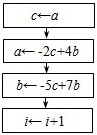 B、
B、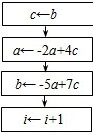
 D、
D、