题目内容
将函数f(x)=2cos(
+
)的图象向左平移
个单位，再向下平移1个单位，得到函数g（x）的图象，则g（x）的解析式为
| x |
| 3 |
| π |
| 6 |
| π |
| 4 |
g(x)=2cos(
+
)-1
| x |
| 3 |
| π |
| 4 |
g(x)=2cos(
+
)-1
．| x |
| 3 |
| π |
| 4 |
分析：直接利用左加右减、上加下减的平移原则，推出平移后的函数解析式即可．
解答：解：将函数f(x)=2cos(
+
)的图象向左平移
个单位，得到f(x)=2cos(
+
)=2cos(
+
)，
再向下平移1个单位，得到函数g(x)=2cos(
+
)-1的图象，所以g（x）的解析式为g(x)=2cos(
+
)-1．
故答案为：g(x)=2cos(
+
)-1．
| x |
| 3 |
| π |
| 6 |
| π |
| 4 |
x+
| ||
| 3 |
| π |
| 6 |
| x |
| 3 |
| π |
| 4 |
再向下平移1个单位，得到函数g(x)=2cos(
| x |
| 3 |
| π |
| 4 |
| x |
| 3 |
| π |
| 4 |
故答案为：g(x)=2cos(
| x |
| 3 |
| π |
| 4 |
点评：本题考查三角函数的图象的平移变换，值域左加右减以及上加下减的法则，值域平移的方向与x的系数的关系．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
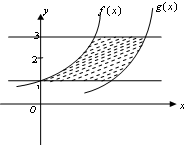将函数f（x）=ax图象向右平移n个单位得函数g（x）的图象，由f（x），g（x）的图象及直线y=1和y=3围成的封闭图形的面积为6，则n=（ ）