题目内容
在△ABC中,若AB=2,AC=3,则“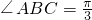 ”是“△ABC为锐角三角形”的
”是“△ABC为锐角三角形”的
- A.充分不必要条件
- B.必要不充分条件
- C.充分且必要条件
- D.既不充分也不必要条件
A
分析:利用正弦定理判断出若“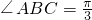 ”成立,能推出“△ABC为锐角三角形”成立,反之若“△ABC为锐角三角形”成立推不出“
”成立,能推出“△ABC为锐角三角形”成立,反之若“△ABC为锐角三角形”成立推不出“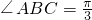 ”成立,利用充要条件的有关定义得到结论.
”成立,利用充要条件的有关定义得到结论.
解答:因为△ABC中,AB=2,AC=3,
若“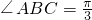 ”成立,则有正弦定理得
”成立,则有正弦定理得
即
即 ,
,
因为AB=2<AC=3,
所以C<B= ,
,
所以C ,
,
所以B+C> ,
,
所以A为锐角,
所以△ABC为锐角三角形;
反之,因为△ABC中,AB=2,AC=3,
若“△ABC为锐角三角形”成立,
有正弦定理得
即 得不出“
得不出“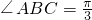 ”成立,
”成立,
所以“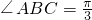 ”是“△ABC为锐角三角形”的充分不必要条件,
”是“△ABC为锐角三角形”的充分不必要条件,
故选A.
点评:本题考查判断一个命题是另一个命题的什么条件,应该先化简各个命题,然后两边互相推一下,利用充要条件的有关定义进行判断,属于中档题.
分析:利用正弦定理判断出若“
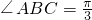 ”成立,能推出“△ABC为锐角三角形”成立,反之若“△ABC为锐角三角形”成立推不出“
”成立,能推出“△ABC为锐角三角形”成立,反之若“△ABC为锐角三角形”成立推不出“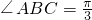 ”成立,利用充要条件的有关定义得到结论.
”成立,利用充要条件的有关定义得到结论.解答:因为△ABC中,AB=2,AC=3,
若“
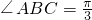 ”成立,则有正弦定理得
”成立,则有正弦定理得
即

即
 ,
,因为AB=2<AC=3,
所以C<B=
 ,
,所以C
 ,
,所以B+C>
 ,
,所以A为锐角,
所以△ABC为锐角三角形;
反之,因为△ABC中,AB=2,AC=3,
若“△ABC为锐角三角形”成立,
有正弦定理得

即
 得不出“
得不出“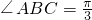 ”成立,
”成立,所以“
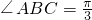 ”是“△ABC为锐角三角形”的充分不必要条件,
”是“△ABC为锐角三角形”的充分不必要条件,故选A.
点评:本题考查判断一个命题是另一个命题的什么条件,应该先化简各个命题,然后两边互相推一下,利用充要条件的有关定义进行判断,属于中档题.

练习册系列答案
相关题目
已知在△ABC中,若
•
=
•
,则△ABC的形状是( )
| AB |
| AC |
| BA |
| BC |
| A、直角三角形 |
| B、正三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知