题目内容
已知二次函数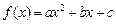 , 满足
, 满足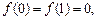 且
且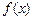 的最小值是
的最小值是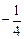 .
.
(1) 求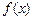 的解析式;
的解析式;
(2) 设直线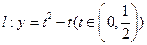 ,若直线
,若直线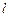 与
与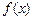 的图象以及
的图象以及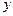 轴所围成封闭图形的面积是
轴所围成封闭图形的面积是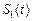 , 直线
, 直线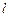 与
与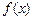 的图象所围成封闭图形的面积是
的图象所围成封闭图形的面积是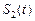 ,设
,设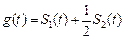 ,当
,当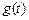 取最小值时,求
取最小值时,求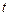 的值.
的值.
(3)已知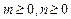 , 求证:
, 求证: 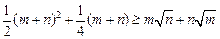 .
.
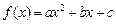 , 满足
, 满足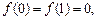 且
且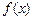 的最小值是
的最小值是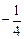 .
.(1) 求
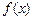 的解析式;
的解析式;(2) 设直线
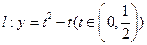 ,若直线
,若直线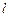 与
与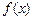 的图象以及
的图象以及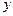 轴所围成封闭图形的面积是
轴所围成封闭图形的面积是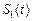 , 直线
, 直线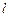 与
与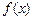 的图象所围成封闭图形的面积是
的图象所围成封闭图形的面积是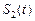 ,设
,设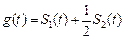 ,当
,当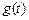 取最小值时,求
取最小值时,求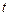 的值.
的值.(3)已知
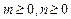 , 求证:
, 求证: 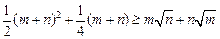 .
.(1) 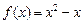
(2)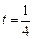
(3)证明略
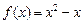
(2)
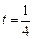
(3)证明略
(1)由二次函数图象的对称性, 可设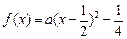 ,又
,又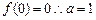
故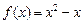 …………………3分
…………………3分
(2) 据题意, 直线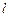 与
与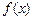 的图象的交点坐标为
的图象的交点坐标为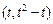 和
和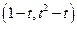 ,由定积分的几何意
,由定积分的几何意
义知 ……5分
……5分
=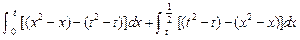
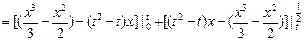
=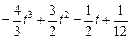 …………………7分
…………………7分
而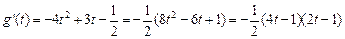
令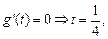 或
或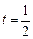 (不合题意,舍去)
(不合题意,舍去)
当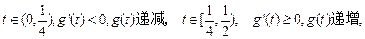 …………………8分
…………………8分
故当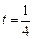 时,
时,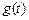 有最小值. ………………………………………………9分
有最小值. ………………………………………………9分
(3)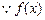 的最小值为
的最小值为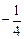
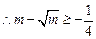 ……①
……①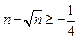 ……② …………………………………………10分
……② …………………………………………10分
由①+②得: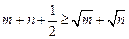
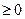 ………③ …………………11分
………③ …………………11分
又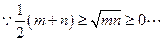
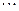 ④ …………………12分
④ …………………12分
故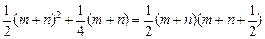
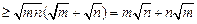 ……13分
……13分
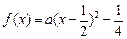 ,又
,又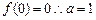
故
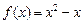 …………………3分
…………………3分(2) 据题意, 直线
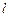 与
与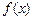 的图象的交点坐标为
的图象的交点坐标为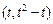 和
和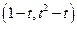 ,由定积分的几何意
,由定积分的几何意义知
 ……5分
……5分=
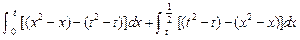
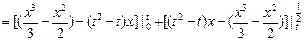
=
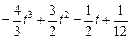 …………………7分
…………………7分而
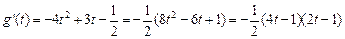
令
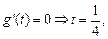 或
或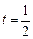 (不合题意,舍去)
(不合题意,舍去)当
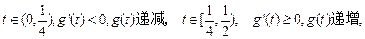 …………………8分
…………………8分故当
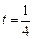 时,
时,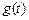 有最小值. ………………………………………………9分
有最小值. ………………………………………………9分(3)
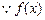 的最小值为
的最小值为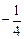
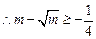 ……①
……①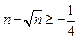 ……② …………………………………………10分
……② …………………………………………10分由①+②得:
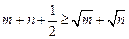
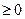 ………③ …………………11分
………③ …………………11分又
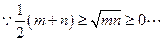
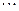 ④ …………………12分
④ …………………12分故
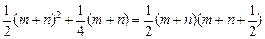
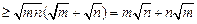 ……13分
……13分
练习册系列答案
相关题目
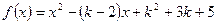 有两个零点;
有两个零点;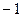 和
和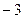 ,求k的值;
,求k的值; ,求
,求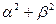 的取值范围.
的取值范围.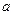 为实数,函数
为实数,函数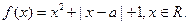
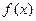 的奇偶性;
的奇偶性;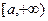 上的最小值.
上的最小值. 上的最小值.
上的最小值.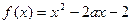 在[ 1,+∞)上单调递增”的( )
在[ 1,+∞)上单调递增”的( ) 对任意
对任意 ( )
( )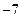
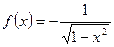 的单调递增区间为 .
的单调递增区间为 .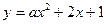 图像恒在x轴上方,则实数
图像恒在x轴上方,则实数 的范围为( )
的范围为( )


 且
且


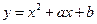 在点
在点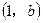 处的切线方程是
处的切线方程是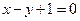 ,则a= b=
,则a= b=