题目内容
(本小题满分14分)
设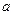 为实数,函数
为实数,函数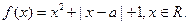
(Ⅰ)讨论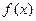 的奇偶性;
的奇偶性;
(Ⅱ)求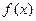 在
在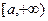 上的最小值.
上的最小值.
(Ⅲ)求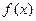 在
在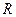 上的最小值.
上的最小值.
设
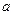 为实数,函数
为实数,函数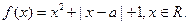
(Ⅰ)讨论
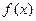 的奇偶性;
的奇偶性;(Ⅱ)求
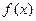 在
在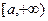 上的最小值.
上的最小值.(Ⅲ)求
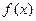 在
在 上的最小值.
上的最小值.(Ⅰ)当 为偶函数.
为偶函数.
当 函数
函数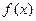 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(Ⅱ)略
(Ⅲ)当
当
当
 为偶函数.
为偶函数.当
 函数
函数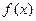 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.(Ⅱ)略
(Ⅲ)当

当

当

解:(Ⅰ)当 为偶函数.
为偶函数.
……2分
当
 .
.
此时函数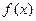 既不是奇函数,也不是偶函数. ……4分
既不是奇函数,也不是偶函数. ……4分
(Ⅱ)(i)当
若 上单调递减,从而,函数
上单调递减,从而,函数 上的最小值为
上的最小值为
若 ,则函数
,则函数 上的最小值为
上的最小值为 ………8分
………8分
(ii)当 时,函数
时,函数
若
若

…12分
综上,当
当
当 ……………14分
……………14分
 为偶函数.
为偶函数.……2分
当

 .
.此时函数
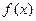 既不是奇函数,也不是偶函数. ……4分
既不是奇函数,也不是偶函数. ……4分(Ⅱ)(i)当

若
 上单调递减,从而,函数
上单调递减,从而,函数 上的最小值为
上的最小值为
若
 ,则函数
,则函数 上的最小值为
上的最小值为 ………8分
………8分(ii)当
 时,函数
时,函数
若

若


…12分
综上,当

当

当
 ……………14分
……………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
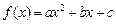 , 满足
, 满足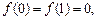 且
且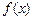 的最小值是
的最小值是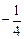 .
.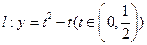 ,若直线
,若直线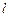 与
与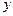 轴所围成封闭图形的面积是
轴所围成封闭图形的面积是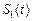 , 直线
, 直线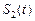 ,设
,设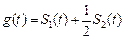 ,当
,当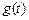 取最小值时,求
取最小值时,求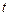 的值.
的值.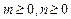 , 求证:
, 求证: 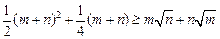 .
. .
. 时,解不等式
时,解不等式 ; (2)若
; (2)若 ,解关于x的不等式
,解关于x的不等式 (
( 为实数)的最小值为
为实数)的最小值为 ,若
,若 ,求
,求
 ,则
,则 = .
= . 数
数 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则 的取值范围是( )
的取值范围是( )





 ,
, 恒成立,则
恒成立,则 的取值范围是 .
的取值范围是 .  若
若 则 ( )
则 ( )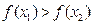


 与
与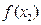 的大小不能确定
的大小不能确定