题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为正三角形,若存在,求出点
为正三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() .(2)在
.(2)在![]() 轴上是存在点
轴上是存在点![]() ,坐标为
,坐标为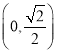 ,
,
【解析】
(1)因为椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,可得
,可得![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() ,故
,故 ,即可求得答案;
,即可求得答案;
(2)设线段![]() 的中点
的中点![]() ,若
,若![]() 是正三角形,
是正三角形,![]() 且
且![]() ,结合已知,即可求得答案.
,结合已知,即可求得答案.
(1)![]() 椭圆
椭圆![]() :
:![]() 的离心率为
的离心率为![]()
![]() ,可得
,可得![]()
故![]()
![]() 右焦点到直线
右焦点到直线![]() 的距离为
的距离为![]() .
.
![]()

①当![]() 时,将
时,将![]() 代入
代入
可得![]()
整理可得:![]()
即![]()
解得:![]() (舍去)或
(舍去)或![]()
由![]() ,可得
,可得![]() ,即
,即![]()
根据![]()
可得:![]()
![]()
![]()
②当![]() 时,将
时,将![]() 代入
代入
可得![]()
整理可得:![]()
![]()
![]()
![]() 方程无解
方程无解
(2)![]() 过点
过点![]() 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线![]()
设直线![]() 的方程为
的方程为![]()
联立直线![]() 的方程和椭圆
的方程和椭圆![]() 方程可得:
方程可得: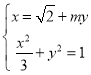 ,消掉
,消掉![]()
可得:![]()
![]()
根据韦达定理可得: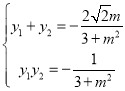
![]()
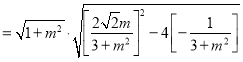
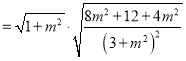
![]()
设线段![]() 的中点
的中点![]() ,
,
则![]() ,
,![]()
![]() 是正三角形
是正三角形
![]()
![]() 且
且![]()
根据![]() ,可得
,可得![]()
![]()
![]()
由![]() 可得:
可得:![]()
![]() 可得:
可得:![]() ,解得:
,解得:![]()
设![]() ,将其代入
,将其代入![]()
可得![]()
可得![]()
故在![]() 轴上是存在点
轴上是存在点![]() ,使得
,使得![]() 为正三角形,坐标为
为正三角形,坐标为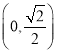 ,
,

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】人们随着生活水平的提高,健康意识逐步加强,健身开始走进人们生活,在健身方面投入越来越多,为了调查参与健身的年轻人一年健身的花费情况,研究人员在![]() 地区随机抽取了参加健身的青年男性、女性各50名,将其花费统计情况如下表所示:
地区随机抽取了参加健身的青年男性、女性各50名,将其花费统计情况如下表所示:
分组(花费) | 频数 |
| 6 |
| 22 |
| 25 |
| 35 |
| 8 |
| 4 |
男性 | 女性 | 合计 | |
健身花费不超过2400元 | 23 | ||
健身花费超过2400元 | 20 | ||
合计 |
(1)完善二联表中的数据;
(2)根据表中的数据情况,判断是否有99%的把握认为健身的花费超过2400元与性别有关;
(3)求这100名被调查者一年健身的平均花费(同一组数据用该区间的中点值代替).
附:![]()
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.01 |
k | 2.706 | 3.841 | 5.024 | 6.635 |