题目内容
设f(x)=cos2x-2a(1+cosx)的最小值为-| 1 | 2 |
分析:根据二倍角余弦公式,将f(x)化为f(x)=2cos2x-1-2a-2acosx=2(cosx-
)2-
a2-2a-1,看作关于cosx的二次函数,再结合二次函数的性质求出最小值的表达式,最后解相应的方程即可.
| a |
| 2 |
| 1 |
| 2 |
解答:解:f(x)=2cos2x-1-2a-2acosx=2(cosx-
)2-
a2-2a-1,∵-1≤cosx≤1
∴(1)a>2时,f(x)当cosx=1时取最小值1-4a;
(2)a<-2时,f(x)当cosx=-1时取最小值1;
(3)-2≤a≤2时,f(x)当cosx=
时取最小值-
a2-2a-1.
又a>2或a<-2时,f(x)的最小值不能为-
,
故-
a2-2a-1=-
,解得a=-2+
,
故答案为-2+
| a |
| 2 |
| 1 |
| 2 |
∴(1)a>2时,f(x)当cosx=1时取最小值1-4a;
(2)a<-2时,f(x)当cosx=-1时取最小值1;
(3)-2≤a≤2时,f(x)当cosx=
| a |
| 2 |
| 1 |
| 2 |
又a>2或a<-2时,f(x)的最小值不能为-
| 1 |
| 2 |
故-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
故答案为-2+
| 3 |
点评:本题考查三角函数性质,二次函数性质,考查分类讨论、转化、计算等能力和方法.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 sinωxcosωx
sinωxcosωx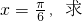 ω的值.
ω的值. sinωxcosωx
sinωxcosωx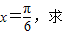 ω的值.
ω的值.