题目内容
1.在△ABC中,记角A,B,C的对边为a,b,c,角A为锐角,设向量$\overrightarrow m$=(cosA,sinA),$\overrightarrow n$=(cosA,-sinA),且$\overrightarrow m$•$\overrightarrow n$=$\frac{1}{2}$(I)求角A的大小及向量$\overrightarrow m$与$\overrightarrow n$的夹角;
(II)若a=$\sqrt{5}$,求△ABC面积的最大值.
分析 (I)在△ABC中,由$\overrightarrow m$•$\overrightarrow n$=$\frac{1}{2}$求得cos2A=$\frac{1}{2}$,可得A的值.再根据两个向量的数量积的定义求得向量$\overrightarrow m$与$\overrightarrow n$的夹角.
(II)由条件利用余弦定理以及基本不等式求得bc的最大值,可得△ABC面积$\frac{1}{2}$bc•sinA的最大值.
解答 解:(I)在△ABC中,由$\overrightarrow m$•$\overrightarrow n$=$\frac{1}{2}$求得cos2A=$\frac{1}{2}$,可得$A=\frac{π}{6}$.
再根据$\overrightarrow m•\overrightarrow n=|\overrightarrow m|•|\overrightarrow{n|}•cos<\overrightarrow{m,}\overrightarrow{n>}=\frac{1}{2}$=cos<$\overrightarrow{m}$,$\overrightarrow{n}$>,求得cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{1}{2}$,
可得向量$\overrightarrow m$与$\overrightarrow n$的夹角<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{π}{3}$.
(II)∵a=$\sqrt{5}$,A=$\frac{π}{6}$,由余弦定理可得a2=5=b2+c2-2bc•cosA≥2bc-$\sqrt{3}$bc,
求得 bc≤10+5$\sqrt{3}$,当且仅当b=c时取等号,故△ABC面积$\frac{1}{2}$bc•sinA=$\frac{bc}{4}$的最大值为$\frac{10+5\sqrt{3}}{4}$.
点评 本题主要考查两个向量的数量积的定义,余弦定理以及基本不等式的应用,属于中档题.

| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(1)请将上表补充完整(不用写计算过程);
(2)请问有多大的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$+3 | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
①命题“p∧q”为真;
②命题“p∧?q”为假;
②命题“¬p∨q”为真;
④命题“¬p∨¬q”为假;
其中正确的命题序号为( )
| A. | ②④ | B. | ②③ | C. | ③④ | D. | ①②③ |
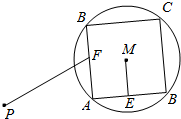 如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )
如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )| A. | [-2,2] | B. | [-2$\sqrt{2}$,2$\sqrt{2}$] | C. | [-4,4] | D. | [-4$\sqrt{2}$,4$\sqrt{2}$] |