题目内容
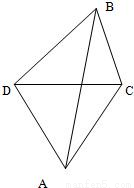
如图，我炮兵阵地位于A处，两观察所分别设于C、D，已知△ACD为边长等于a的正三角形．若目标出现于B时，测得∠CDB=45°，∠BCD=75°，则炮击目标AB的距离为
|
|
分析：在△BCD中利用正弦定理，利用∠DBC和a求得BC的值，进而在△ABC中利用BC和a，根据余弦定理求得AB．
解答：解：在△BCD中，∠DBC=60°，
=
，
∴BC=
a，
在△ABC中，∠BCA=135°，
AB2=（
a）2+a2-2×
a×a×cos135°=
a，
∴AB=
a．
故炮击目标的距离AB为
a．
故答案为：
a．
| a |
| sin60° |
| BC |
| sin45° |
∴BC=
| ||
| 3 |
在△ABC中，∠BCA=135°，
AB2=（
| ||
| 3 |
| ||
| 3 |
5+2
| ||
| 3 |
∴AB=
|
故炮击目标的距离AB为
|
故答案为：
|
点评：本题考查解三角形的实际应用．解三角形问题常用正弦定理，余弦定理，三角形面积公式等来解决，平时应注意这方面的积累，属于中档题．
练习册系列答案
相关题目
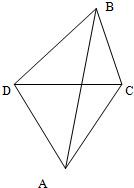如图，我炮兵阵地位于A处，两观察所分别设于C，D，已知△ACD为边长等于a的正三角形．当目标出现于B时，测得∠CDB=45°，∠BCD=75°，试求炮击目标的距离AB．（结果保留根式形式）
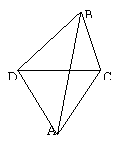如图，我炮兵阵地位于A处，两观察所分别设于C，D，已知△ACD为边长等于
的正三角形．当目标出现于B时，测得∠CDB＝45°,∠BCD＝75°，试求炮击目标的距离AB．（结果保留根式形式）
