题目内容
10.在△ABC中,内角A,B,C的对边分别是a,b,c,且$\frac{sinC}{sinA-sinB}$=$\frac{a+b}{a-c}$.(Ⅰ)求角B的大小;
(Ⅱ)点D满足$\overrightarrow{BD}$=2$\overrightarrow{BC}$,且线段AD=3,求2a+c的最大值.
分析 (Ⅰ)由正弦定理和余弦定理,即可求出cosB以及B的值;
(Ⅱ)结合题意画出图形,根据图形利用余弦定理和基本不等式,即可求出2a+c的值.
解答 解:(Ⅰ)△ABC中,$\frac{sinC}{sinA-sinB}$=$\frac{a+b}{a-c}$,
∴$\frac{c}{a-b}$=$\frac{a+b}{a-c}$,
∴ac-c2=a2-b2,
∴ac=a2+c2-b2,
∴cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$;
又B∈(0,π),
∴B=$\frac{π}{3}$;
(Ⅱ)如图所示,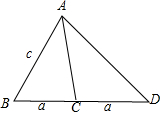
点D满足$\overrightarrow{BD}$=2$\overrightarrow{BC}$,∴BC=CD;
又线段AD=3,
∴AD2=c2+4a2-2•c•2acos$\frac{π}{3}$=c2+4a2-2ac=9,
∴c2+4a2=9+2ac;
又c2+4a2≥2c•2a,
∴4ac≤9+2ac,
∴2ac≤9;
∴(2a+c)2=4a2+4ac+c2=9+6ac≤9+3×9=36,
∴2a+c≤6,
即2a+c的最大值为6.
点评 本题考查了正弦定理和余弦定理的应用问题,也考查了基本不等式的应用问题,是综合题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
1.某几何体的三视图如图所示,其中正视图是半径为1的半圆,则该几何体的表面积是( )


| A. | $\frac{{(\sqrt{5}-1)π}}{2}+2$ | B. | $\frac{{(\sqrt{5}+1)π}}{2}+2$ | C. | $\frac{π}{2}+3$ | D. | $\frac{{\sqrt{5}}}{2}π+2$ |
5.函数f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为π,其图象关于直线x=$\frac{π}{3}$对称,则|φ|的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{5π}{12}$ |
15.已知函数f(x)的图象关于x=-1对称,且f(x)在(-1,+∞)上单调,若数列{an}是公差不为0的等差数列,且f(a50)=f(a51),则{an}的前100项的和为( )
| A. | -200 | B. | -100 | C. | -50 | D. | 0 |
2.已知命题p:若a>|b|,则a2>b2;命题q:若x2=4,则x=2,.下列说法正确的是( )
| A. | “p∨q”为假命题 | B. | “p∧q”为假命题 | C. | “¬p”为真命题 | D. | “¬q”为假命题 |
20.若实数x,y满足不等式组$\left\{\begin{array}{l}x-2y+2≥0\\ x+2y+2≥0\\ 2x-y-1≤0\end{array}\right.$,则2|x+1|+y的最大值是( )
| A. | $\frac{14}{3}$ | B. | $\frac{19}{3}$ | C. | 4 | D. | 1 |