题目内容
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
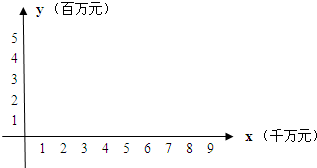
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.参考公式:回归直线的方程
是:
| ? |
| y |
| |||||||
|
. |
| y |
. |
| x |
| ? |
| yi |
分析:(1)根据连锁经营公司所属5个零售店某月的销售额和利润额资料作出散点图,由散点图知两个变量符合正相关.
(2)设回归直线的方程是
=bx+a,分别求出
,
,由b=
,a=
-b
,能求出利润额y对销售额x的回归直线方程.
(3)由利润额y对销售额x的回归直线方程,能求出当销售额为4千万元时的利润额.
(2)设回归直线的方程是
 |
| y |
. |
| x |
. |
| y |
| |||||||
|
. |
| y |
. |
| x |
(3)由利润额y对销售额x的回归直线方程,能求出当销售额为4千万元时的利润额.
解答:解:(1)根据连锁经营公司所属5个零售店某月的销售额和利润额资料作出散点图:

由散点图知两个变量符合正相关. …(4分)
(五个点中,有错的,不能得(2分),有两个或两个以上对的,至少得1分)
(2)设回归直线的方程是:
=bx+a,
=6,
=3.4;…(6分)
∴b=
=
=
=
…(10分)a=0.4
∴y对销售额x的回归直线方程为:y=0.5x+0.4…(12分)
(3)当销售额为4(千万元)时,利润额为:
=0.5×4+0.4=2.4(百万元) …(14分)

由散点图知两个变量符合正相关. …(4分)
(五个点中,有错的,不能得(2分),有两个或两个以上对的,至少得1分)
(2)设回归直线的方程是:
| ? |
| y |
. |
| x |
. |
| y |
∴b=
| |||||||
|
| -3×(-1.4)+(-1)×(-0.4)+1×0.6+3×1.6 |
| 9+1+1+9 |
| 10 |
| 20 |
| 1 |
| 2 |
…(10分)a=0.4
∴y对销售额x的回归直线方程为:y=0.5x+0.4…(12分)
(3)当销售额为4(千万元)时,利润额为:
| ? |
| y |
点评:本题考查线性回归方程,解题的关键是掌握住线性回归方程中系数的求法公式及线性回归方程的形式,按公式中的计算方法求得相关的系数,得出线性回归方程,本题考查了公式的应用能力及计算能力,求线性回归方程运算量较大,解题时要严谨,莫因为计算出错导致解题失败.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
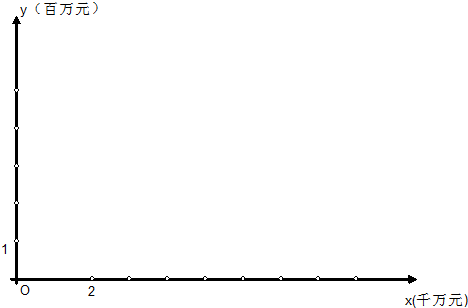
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.