Question

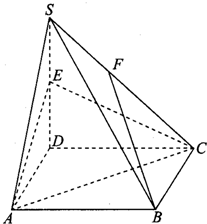如图，在四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，E是SD的中点，AD=

2

，DC=SD=2．
（1）证明：SB∥平面ACE；
（2）求二面角A-SB-C的余弦值；
（3）设点F在侧棱SC上，∠ABF=60°，求

SF

FC

．

Answer 1

分析：（1）由已知中SD⊥底面ABCD，底面ABCD为矩形，易得DA，DC，DS两两垂直，以D为原点，直线DA，DC，DS分别为x，y，z轴，建立空间直角坐标系．求出向量

SB

，

EO

的坐标，易得

SB

与

EO

平行，进而由线面垂直的判定定理得到SB∥平面ACE；
（2）求出平面CBS的一个法向量和平面ABS的一个法向量，代入向量夹角公式，易求出二面角A-SB-C的余弦值；
（3）设

SF

=λ

FC

（λ＞0），由已知中∠ABF=60°，我们可根据向量夹角公式，构造一个关于λ的方程，解方程求出λ的值，即可得到

SF

FC

．

解答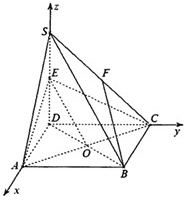：解：∵SD⊥底面ABCD，底面ABCD为矩形，
∴DA，DC，DS两两垂直，
如图以D为原点，直线DA，DC，DS分别为x，y，z轴，建立空间直角坐标系．
则D（0，0，0），B（

2

，2，0），S（0，0，2），C（0，2，0），
又∵E是SD的中点，
∴E（0，0，1）
证明：（1）连接BD，与AC相交于点O，连接EO
所以O（

2

2

，1，0）
∵

EO

=（

2

2

，1，-1），

SB

=（

2

，2，-2），
∴

SB

=2

EO

∴SB∥EO
∵EO?平面ACE，SB?平面ACE，
∴SB∥平面ACE；
解：（2）设

u

=（a，b，c）是平面CBS的一个法向量，则

u

•

BC

=0，

u

•

SC

=0
∵

BC

=（-

2

，0，0），

SC

=（0，2，-2）
∴

- 2 a=0 2b-2c=0

，令b=1，则

u

=（0，1，1）
同理可得

v

=（

2

，0，-2）是平面ABS的一个法向量，
则钝二面角A-SB-C的夹角θ，则
|cosθ|=

u • v

| u |•| v |

=

6

6

∴二面角A-SB-C的余弦值是-

6

6

证明：（3）设

SF

=λ

FC

（λ＞0）
则F（0，

2λ

1+λ

，

2

1+λ

），

BF

=（-

2

，

-2

1+λ

，

2

1+λ

），
又∵

BA

=（0，-2，0），＜

BA

，

BF

＞=∠ABF=60°，
故

BA

•

BF

=|

BA

|•|

BF

|•cos60°
即

4

1+λ

=

(- 2 )2+( -2 1+λ )2+( 2 1+λ )2

解得λ=1
∴

SF

FC

=1

点评：本题考查的知识点是用空间向量求平面间的夹角，平面向量数量积的运算，向量语言表述线面的垂直、平行关系，其中（1）的关键是证得向量

SB

与

EO

平行，（2）中易忽略二面角A-SB-C为钝二面角，而错解为

6

6

，（3）的关键是根据向量夹角公式，构造一个关于λ的方程．