题目内容
(本小题8分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直. EF//AC,AB=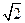 ,CE=EF=1,
,CE=EF=1,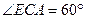 .
.
(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.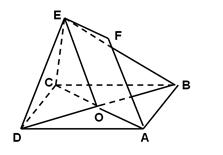
如图,正方形ABCD和四边形ACEF所在的平面互相垂直. EF//AC,AB=
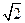 ,CE=EF=1,
,CE=EF=1,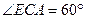 .
.(1)求证:AF//平面BDE;
(2)求异面直线AB与DE所成角的余弦值.

(1)略
(2)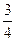
(2)
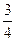
(1)证明: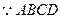 是正方形,且AB=
是正方形,且AB=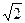 ,
, AO=1,又
AO=1,又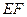 //
//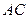 ,EF=1,
,EF=1,
 EFAO为平行四边形,则
EFAO为平行四边形,则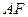 //
//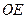 ,而
,而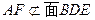 ,
,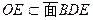 ,
,
 AF//面BDE ………………………………………………(3分)
AF//面BDE ………………………………………………(3分)
(2)解: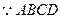 是正方形,
是正方形,
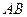 //
//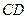

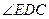 为异面直线AB与DE所成的角或其补角 …………………………(2分)
为异面直线AB与DE所成的角或其补角 …………………………(2分)
又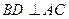 ,又面ABCD
,又面ABCD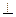 面ACEF,且面ABCD
面ACEF,且面ABCD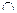 面ACEF=AC
面ACEF=AC
 BD
BD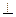 面ACEF,又
面ACEF,又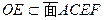 ,
, BD
BD OE.
OE.
而由EC=1,OC=OA=1,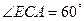
 OE=1,又OD=1,则ED=
OE=1,又OD=1,则ED=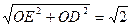
又CD=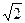 ,CE="1,"
,CE="1," 
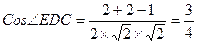
 异面直线AB与DE所成的角的余弦值为
异面直线AB与DE所成的角的余弦值为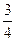 ……………………………………(3分)
……………………………………(3分)
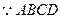 是正方形,且AB=
是正方形,且AB=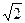 ,
, AO=1,又
AO=1,又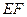 //
//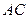 ,EF=1,
,EF=1, EFAO为平行四边形,则
EFAO为平行四边形,则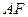 //
//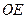 ,而
,而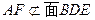 ,
,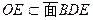 ,
, AF//面BDE ………………………………………………(3分)
AF//面BDE ………………………………………………(3分)(2)解:
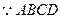 是正方形,
是正方形,
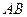 //
//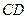

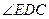 为异面直线AB与DE所成的角或其补角 …………………………(2分)
为异面直线AB与DE所成的角或其补角 …………………………(2分)又
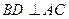 ,又面ABCD
,又面ABCD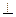 面ACEF,且面ABCD
面ACEF,且面ABCD 面ACEF=AC
面ACEF=AC BD
BD 面ACEF,又
面ACEF,又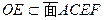 ,
, BD
BD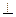 OE.
OE.而由EC=1,OC=OA=1,
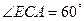
 OE=1,又OD=1,则ED=
OE=1,又OD=1,则ED=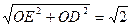
又CD=
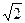 ,CE="1,"
,CE="1," 
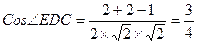
 异面直线AB与DE所成的角的余弦值为
异面直线AB与DE所成的角的余弦值为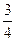 ……………………………………(3分)
……………………………………(3分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
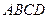 和矩形
和矩形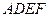 所在平面相互垂直,
所在平面相互垂直,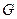 是
是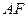 的中点.
的中点.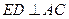 ;
; 与平面
与平面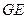 与
与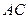 所成角的余弦值.
所成角的余弦值.
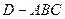 中,已知△
中,已知△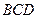 是正三角形,
是正三角形,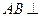 平面
平面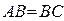 ,
,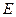 为
为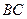 的中点,
的中点,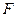 在棱
在棱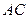 上,且
上,且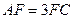 ,
, 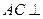 平面
平面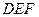 ;
;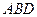 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;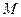 为
为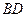 的中点,问
的中点,问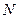 ,使
,使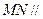 平面
平面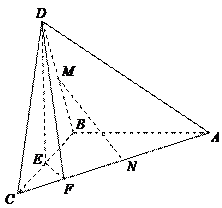
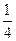 ,并求此时二面角A—PC—B的余弦值。
,并求此时二面角A—PC—B的余弦值。
 的四个顶点均在半径为
的四个顶点均在半径为 的球面上,且满足
的球面上,且满足 ,
, ,
, ,则三棱锥
,则三棱锥


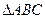 为正三角形,
为正三角形,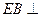 平面ABC,AD//BE,且BE=AB+2AD,P是EC的中点。
平面ABC,AD//BE,且BE=AB+2AD,P是EC的中点。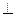 平面PBD。
平面PBD。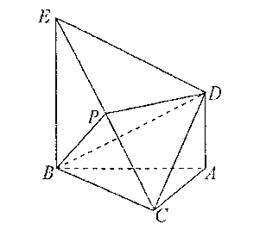
 ,
, ,
, 满足,
满足, ,
, ,
, 和
和 ,那么必有
,那么必有 且
且

 且
且