题目内容
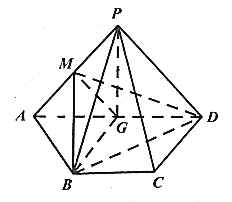
【题目】已知A、B、C是不共线的三点，O是平面ABC外一点，则在下列条件中，能得到点M与A、B、C一定共面的条件是（ ）
A.
B.
C.
D.
【答案】C
【解析】
由共面向量定理可得：若定点
与点
、
、
一定共面，则存在实数
，
，使得
，即
，判断标准是验证
，
，
三个向量的系数和是否为1，若为1则说明四点，，，一定共面，由此规则即可找出正确的条件．
由题意
三点不共线，点
是平面
外一点，
对于A由于向量的系数和是
，不是1，故此条件不能保证点在面上；
对于B，等号右边三个向量的系数和为3，不满足四点共面的条件，故不能得到点与一定共面
对于C，等号右边三个向量的系数和为1，满足四点共面的条件，故能得到点与一定共面
对于D，等号右边三个向量的系数和为0，不满足四点共面的条件，故不能得到点与一定共面
综上知，能得到点与一定共面的一个条件为.
故选：．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
