题目内容
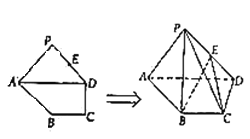
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() .
.
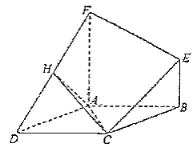
(Ⅰ)证明:![]() 平面
平面![]() .
.
(Ⅱ)若平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,求平面
的中点,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(I)见解析;(II)![]()
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,结合已知条件,得四边形
,结合已知条件,得四边形![]() 为平行四边形,进而得
为平行四边形,进而得![]() 为平行四边形,由线面平行的判定定理得CE∥平面ADF.
为平行四边形,由线面平行的判定定理得CE∥平面ADF.
(Ⅱ)取CD中点N,以A为原点,AN为x轴,AB为y轴,AF为z轴,建立空间直角坐标系,利用向量法能求出平面ACH与平面ABEF所成锐二面角的余弦值.
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,如图所示,因为
,如图所示,因为![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,
得![]() 且
且![]() ,所以四边形
,所以四边形![]() 为平行四边形,即
为平行四边形,即![]() 且
且![]() .
.
又因为四边形![]() 是菱形,所以
是菱形,所以![]() ,进而
,进而![]() ,得
,得![]() 为平行四边形,
为平行四边形,
即有![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
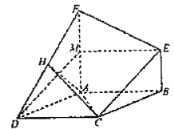
(Ⅱ)取![]() 的中点
的中点![]() ,在菱形
,在菱形![]() 中,
中,![]() ,可得
,可得![]() .因为平面
.因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
以![]() 为坐标原点,AN为x轴,AB为y轴,AF为z轴,建立空间直角坐标系
为坐标原点,AN为x轴,AB为y轴,AF为z轴,建立空间直角坐标系![]() ,如图所示.
,如图所示.
故![]() ,
,![]() ,
,![]() ,
,![]() ,
,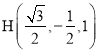 ,
,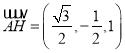 ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有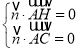 即
即
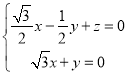 令
令![]() 可得
可得![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,则
,则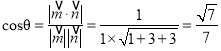 ,
,
即所求二面角的余弦值为![]() .
.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】(2014·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?