题目内容
如图,正方形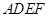 与梯形
与梯形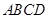 所在的平面互相垂直,
所在的平面互相垂直,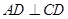 ,
,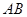 ∥
∥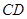 ,
,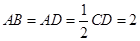 ,点
,点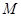 在线段
在线段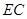 上.
上.
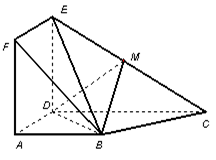
(I)当点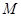 为
为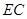 中点时,求证:
中点时,求证: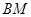 ∥平面
∥平面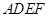 ;
;
(II)当平面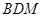 与平面
与平面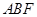 所成锐二面角的余弦值为
所成锐二面角的余弦值为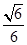 时,求三棱锥
时,求三棱锥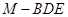 的体积.
的体积.
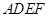 与梯形
与梯形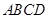 所在的平面互相垂直,
所在的平面互相垂直,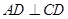 ,
,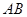 ∥
∥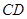 ,
,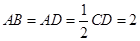 ,点
,点 在线段
在线段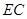 上.
上.
(I)当点
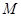 为
为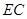 中点时,求证:
中点时,求证: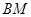 ∥平面
∥平面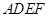 ;
;(II)当平面
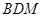 与平面
与平面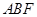 所成锐二面角的余弦值为
所成锐二面角的余弦值为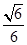 时,求三棱锥
时,求三棱锥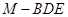 的体积.
的体积.(I)建立空间直角坐标系,证明 ,进而得证;(II)
,进而得证;(II)
 ,进而得证;(II)
,进而得证;(II)
试题分析:
(I )以直线DA,BC,DE分别为x轴,y轴,z轴建立空间直角坐标系,
则
 ,所以
,所以 ,
,所以
 , 2分
, 2分又
 是平面
是平面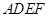 的一个法向量,
的一个法向量, ,所以
,所以 ,
,所以
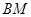 ∥平面
∥平面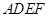 . 4分
. 4分(II)设
 ,则
,则 ,又
,又 ,
,则
 ,
, ,
,取
 得
得  , 即
, 即  ,
,又由题设,
 是平面
是平面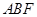 的一个法向量, 8分
的一个法向量, 8分∴
 10分
10分即点
 为
为 中点,此时,
中点,此时, ,
, 为三棱锥
为三棱锥 的高,
的高,∴

 . 12分
. 12分点评:解决立体几何问题,可以用相关的定理证明,也可以用空间向量证明,利用空间向量也要依据相应的判定定理和性质定理,并且要注意各个角的取值范围.

练习册系列答案
相关题目
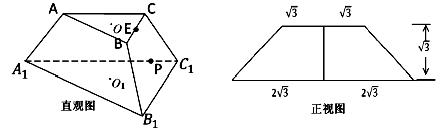
 中,
中, 底面
底面 ,
, ,
, ,
, ,
,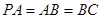 .
.
 平面
平面 ;
; ,并说明理由.
,并说明理由.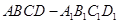 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有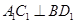 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)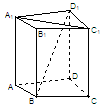
 中,
中, ,
, ,
, 是角平分线。求证:
是角平分线。求证: 。
。
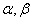 为两个平面,
为两个平面,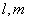 为两条直线,且
为两条直线,且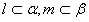 ,有如下两个命题:
,有如下两个命题: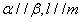 ;②若
;②若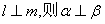 . 那么( )
. 那么( ) ,若
,若 ,且
,且 相交但不垂直,
相交但不垂直, 分别为
分别为 内的直线,则( )
内的直线,则( )


