题目内容
19. 如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
分析 设出球的半径,利用棱锥的体积公式,求解半径,然后求解半球的体积.
解答 解:设球的半径为r,由题意可知SO=AO=OC=OD=OB=r.
则AB=$\sqrt{2}r$,
四棱锥的体积为:$\frac{1}{3}(\sqrt{2}r)^{2}×r$=$\frac{4\sqrt{2}}{3}$,
解得r=$\sqrt{2}$,
半球的体积为:$\frac{2π}{3}{r}^{2}$=$\frac{4\sqrt{2}π}{3}$.
故答案为:$\frac{4\sqrt{2}π}{3}$.
点评 本题考查四棱锥SABCD的体积的计算,确定球的半径关系式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知抛物线C:y2=8x焦点为F,点P是C上一点,若△POF的面积为2,则|PF|=( )
| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
9.设a=tan$\frac{3}{4}$π,b=cos$\frac{2}{5}$π,c=(1+sin$\frac{6}{5}$π)0,则a,b,c的大小关系是( )
| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
 如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.
如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.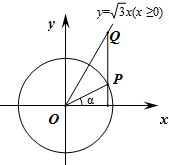 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).