题目内容
8.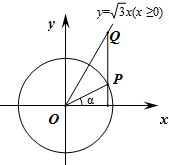 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).(Ⅰ)若sinα=$\frac{1}{3}$,求cos∠POQ;
(Ⅱ)求$\overrightarrow{OP}$•$\overrightarrow{OQ}$的最大值.
分析 (Ⅰ)易得$∠POQ=\frac{π}{3}-α$,由三角函数的和差公式即可计算;
(Ⅱ)用坐标表示出点P、Q,利用辅助角公式将式子进行化简,结合三角函数的图象和性质即可求出数量积的最大值.
解答 解:(Ⅰ)∵sinα=$\frac{1}{3}$,$α∈(-\frac{π}{2},\frac{π}{2})$,
∴$cosα=\frac{2\sqrt{2}}{3}$,$α<\frac{π}{3}$.
∵∠MOQ=$\frac{π}{3}$,且$α<\frac{π}{3}$,
∴$∠POQ=\frac{π}{3}-α$,
∴cos∠POQ=$cos(\frac{π}{3}-α)$=$cos\frac{π}{3}cosα+sin\frac{π}{3}sinα$=$\frac{2\sqrt{2}+\sqrt{3}}{6}$;
(Ⅱ)∵P(cosα,sinα),
∴Q(cosα,$\sqrt{3}cosα$)
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$=$co{s}^{2}α+\sqrt{3}sinα•cosα$=$\frac{1}{2}cos2α+\frac{\sqrt{3}}{2}sin2α+\frac{1}{2}$=$sin(2α+\frac{π}{6})+\frac{1}{2}$,
∵$α∈(-\frac{π}{2},\frac{π}{2})$,
∴$-\frac{5π}{6}<2α+\frac{π}{6}<\frac{7π}{6}$,
所以,当$2α+\frac{π}{6}=\frac{π}{2}$,即$α=\frac{π}{6}$时,$\overrightarrow{OP}•\overrightarrow{OQ}$取最大值$\frac{3}{2}$.
点评 本题主要考查三角函数的定义以及两角和差公式的应用,以及向量数量积的计算,根据三角函数的定义求出点P、Q的坐标是解决本题的关键.

| A. | 甲合适 | B. | 乙合适 | ||
| C. | 油价先高后低甲合适 | D. | 油价先低后高甲合适 |
 如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$. 如图,在正三棱柱ABC-A1B1C1中,D为AB的中点,AA1=4,AB=6,则异面直线B1D与AC1所成角的余弦值为$\frac{5\sqrt{13}}{26}$.
如图,在正三棱柱ABC-A1B1C1中,D为AB的中点,AA1=4,AB=6,则异面直线B1D与AC1所成角的余弦值为$\frac{5\sqrt{13}}{26}$.