题目内容
(本题满分10分)
(Ⅰ)设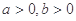 ,求证:
,求证: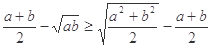 ;
;
(Ⅱ)设 ,求证:三数
,求证:三数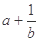 ,
,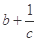 ,
, 中至少有一个不小于2.
中至少有一个不小于2.
(Ⅰ)利用分析法证明即可,(Ⅱ)利用反证法证明
解析试题分析:(Ⅰ)证法一:要证:
即证:
即证:
即证:
由基本不等式,这显然成立,故原不等式得证 5’
证法二:要证:
即证:
由基本不等式 ,可得上式成立,故原不等式得证. 5’
,可得上式成立,故原不等式得证. 5’
(Ⅱ)三数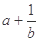 ,
,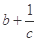 ,
, 都小于2,因为(
都小于2,因为(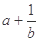 )+(
)+( )+(
)+( )=
)= ,所以矛盾,故假设不成立即原命题成立
,所以矛盾,故假设不成立即原命题成立
考点:本题考查了不等式的证明
点评:应用分析法,一方面要注意寻找使结论成立的充分条件,另一方面要有目的性,逐步逼近已知条件或必然结论.

练习册系列答案
相关题目
不等式组 ,所表示的平面区域的面积等于( )
,所表示的平面区域的面积等于( )
A. | B. | C. | D. |
x , y满足约束条件 若z=y-ax取得最大值的最优解不唯一,则实数a的值为( )
若z=y-ax取得最大值的最优解不唯一,则实数a的值为( )
A. 或-1 或-1 | B.2或 |
| C.2或1 | D.2或-1 |
在约束条件 下,当
下,当 时,目标函数
时,目标函数 的最大值的变化范围是( )
的最大值的变化范围是( )
A. | B. | C. | D. |
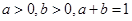 求证:
求证: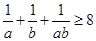
 ,求证:
,求证:
 米的过程中,速度为
米的过程中,速度为 米/分,每分钟
米/分,每分钟 ,其中h为高,r、R分
,其中h为高,r、R分