题目内容
设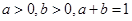 求证:
求证: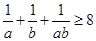
可以运用多种方法。
解析试题分析:证明[法一]:
 2分
2分 10分
10分
当且仅当 ,取“=”号。 11分
,取“=”号。 11分
故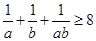 12分
12分
证明[法二]:


当且仅当 ,取“=”号。
,取“=”号。
故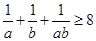
证明[法三]:



当且仅当 ,取“=”号。
,取“=”号。
故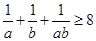
证明[法四]:



当且仅当 时,取“=”号。
时,取“=”号。
故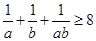
证明[法五]:
∴设
则




当且仅当 时,取“=”号。
时,取“=”号。
故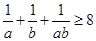
证明[法六]:
∴设
则





当且仅当 时,取“=”号。
时,取“=”号。
故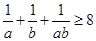
证明[法七]



考点:不等式的证明。
点评:中档题,本题给出了七种证明方法,反映数学知识应用的灵活性,证明方法的多样性,能开拓学生的视野,启迪学生的思路。

练习册系列答案
相关题目
不在3x+2y<6表示的平面区域内的一个点是( )
| A.(0,0) | B.(1,1) | C.(0,2) | D.(2,0) |
已知变量x,y满足约束条件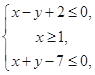 则
则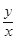 的取值范围是( )
的取值范围是( )
A.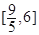 | B. | C.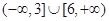 | D.(3,6] |
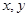 满足
满足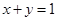 ,求
,求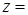
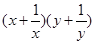 的最小值.
的最小值. ,且
,且 .
. ;
; 恒成立,求实数
恒成立,求实数 的最大值.
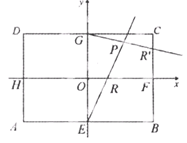
的最大值.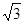 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且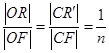 .
.
 :
: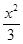 +
+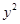 =1上;
=1上;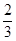 ,求证:直线MN过定点;并求△GMN面积的最大值.
,求证:直线MN过定点;并求△GMN面积的最大值.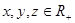 求证:
求证: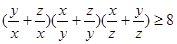
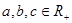 且
且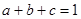 ,求证:
,求证: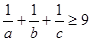
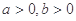 ,求证:
,求证: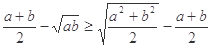 ;
; ,求证:三数
,求证:三数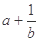 ,
,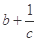 ,
, 中至少有一个不小于2.
中至少有一个不小于2. ≤a恒成立,求a的取值范围.
≤a恒成立,求a的取值范围.