题目内容
(14分)2006年5月3日进行抚仙湖水下考古,潜水员身背氧气瓶潜入湖底进行
考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所
给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下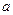 米的过程中,速度为
米的过程中,速度为 米/分,每分钟
米/分,每分钟
需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,
每分钟需氧量为0.4 L;返回水面时,速度也为 米/分,每分钟需氧量为0.2 L,若下
米/分,每分钟需氧量为0.2 L,若下
潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积
计算精确到1 L,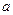 、p为常数,圆台的体积V=
、p为常数,圆台的体积V= ,其中h为高,r、R分
,其中h为高,r、R分
别为上、下底面半径.)
解: 氧气瓶中氧气的体积
V=
 17 L.
17 L.
设潜入水下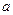 米过程中的每分钟需氧量为Q,则Q=k
米过程中的每分钟需氧量为Q,则Q=k 2,
2,
因当速度为1 m/分时,每分钟需氧量0.2 L,所以k=0.2,
故来回途中需氧量为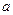 ×0.2
×0.2 +
+ ,则在湖底的工作时间为
,则在湖底的工作时间为
当且仅当, =1时取等号.
=1时取等号.
所以①当p≥1时, 的最大值是42.5-
的最大值是42.5-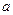 .
.
②当p<1时,
 -
-
即当 时,在湖底的工作时间的最大值为
时,在湖底的工作时间的最大值为
因此,当p≥1时,潜水员在湖底最多能工作42.5-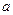 分钟;
分钟;
当p<l时,潜水员在湖底最多能工作 分钟.
分钟.
解析

练习册系列答案
相关题目
不在3x+2y<6表示的平面区域内的一个点是( )
| A.(0,0) | B.(1,1) | C.(0,2) | D.(2,0) |
若x、y满足约束条件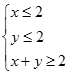 ,则z=x+2y的取值范围( )
,则z=x+2y的取值范围( )
| A.[2,6] | B.[2,5] | C.[3,6] | D.(3,5] |
若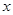 、
、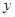 满足
满足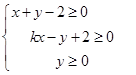 ,且
,且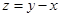 的最小值为
的最小值为 ,则
,则 的值为( )
的值为( )
| A.2 | B.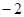 | C. | D.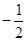 |
 ,(x>0,
,(x>0,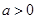 ).
).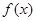 >-x+4,求实数
>-x+4,求实数 的取值范围
的取值范围 ,且
,且 .
. ;
; 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.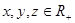 求证:
求证: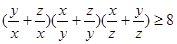
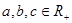 且
且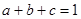 ,求证:
,求证: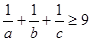
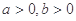 ,求证:
,求证: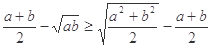 ;
; ,求证:三数
,求证:三数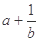 ,
,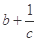 ,
, 中至少有一个不小于2.
中至少有一个不小于2.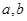 为正数,且
为正数,且 .求
.求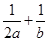 的最小值.
的最小值.