题目内容
甲、乙、丙三名射击运动员射中目标的概率分别为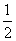 、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.
、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.
(1) 求ξ的分布列及数学期望;
(2) 在概率P(ξ=i)(i=0、1、2、3)中,若P(ξ=1)的值最大,求实数a的取值范围.
解:(1) P(ξ)是“ξ个人命中,3-ξ个人未命中”的概率.其中ξ的可能取值为0、1、2、3.
P(ξ=0)=C
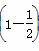 C
C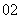 (1-a)2=
(1-a)2=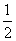 (1-a)2;
(1-a)2;
P(ξ=1)=C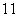 ·
·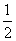 C
C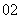 (1-a)2+C
(1-a)2+C
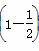 C
C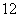 a(1-a)
a(1-a)
=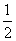 (1-a2);
(1-a2);
P(ξ=2)=C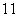 ·
·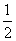 C
C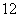 a(1-a)+
a(1-a)+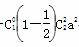
=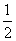 (2a-a2);
(2a-a2);
P(ξ=3)=C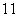 ·
·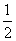 C
C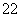 a2=
a2=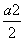 .
.
所以ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
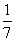 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.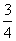 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、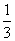 ,则方差V(X)的值是________.
,则方差V(X)的值是________.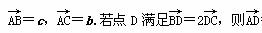 =________.(用b、c表示)
=________.(用b、c表示)