题目内容
3.已知椭圆的两焦点坐标分别是(-2,0)、(2,0),并且过点(2$\sqrt{3}$,$\sqrt{3}$),则该椭圆的标准方程是$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.分析 设出椭圆方程,利用焦点坐标以及椭圆经过的点,列出方程求解即可.
解答 解:椭圆的两焦点坐标分别是(-2,0)、(2,0),可得c=2,
设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-4}=1$,椭圆经过点(2$\sqrt{3}$,$\sqrt{3}$),
可得:$\frac{12}{{a}^{2}}+\frac{3}{{a}^{2}-4}=1$,解得a=4,
则该椭圆的标准方程是:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
故答案为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
点评 本题考查椭圆的简单性质以及椭圆方程的求法,考查计算能力.

练习册系列答案
相关题目
18.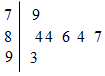 如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
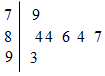 如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是2013年中央电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,1.6 | B. | 84,4 | C. | 84,1.6 | D. | 85,4 |
 已知点F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,点M,P分别是线段F1N,F2N上的点,且满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.
已知点F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,点M,P分别是线段F1N,F2N上的点,且满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.