题目内容
设数列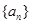 满足:
满足: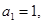 点
点 均在直线
均在直线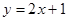 上.
上.
(I)证明数列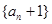 为等比数列,并求出数列
为等比数列,并求出数列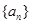 的通项公式;
的通项公式;
(II)若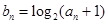 ,求数列
,求数列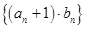 的前
的前 项和
项和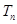 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(I)先由已知变形得 ,从而数列
,从而数列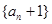 是等比数列,先得到
是等比数列,先得到 的表达式进而可求
的表达式进而可求 ;(Ⅱ)由(I)及已知可先得
;(Ⅱ)由(I)及已知可先得 ,再根据和式的结构特征选择错位相减法求和.
,再根据和式的结构特征选择错位相减法求和.
试题解析:(I)证明:由点 均在直线
均在直线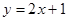 上可知
上可知



于是
即数列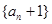 是以
是以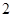 为公比的等比数列.
为公比的等比数列. 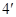
因为 ,所以
,所以
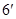
(II) ,所以
,所以
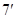
 ①
① 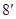

 ②
② 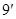
① ②得
②得



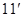
故
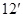
考点:1、数列通项公式的求法;2、数列前 项和的求法.
项和的求法.

练习册系列答案
相关题目
 }中,a1=1,
}中,a1=1, 是数列{
是数列{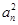 +p
+p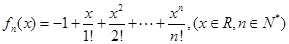
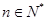 ,存在唯一的
,存在唯一的 ,满足
,满足 ;
;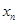 构成数列
构成数列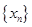 ,判断数列
,判断数列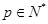 ,
,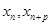 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与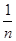 的大小.
的大小.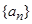 的前
的前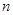 项和为
项和为 ,对任意
,对任意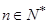 满足
满足 ,且
,且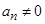 .
. ,求数列
,求数列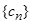 的前
的前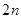 项和
项和 .
.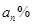 ,B喷雾器中药水的浓度为
,B喷雾器中药水的浓度为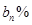 .
.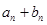 是一个常数;
是一个常数; 与
与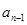 的关系式;
的关系式; 的前三项和为18,
的前三项和为18,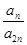 是一个与
是一个与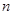 无关的常数,若
无关的常数,若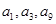 恰为等比数列
恰为等比数列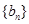 的前三项,(1)求
的前三项,(1)求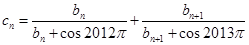 ,
,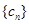 的前三
的前三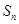 ,求证:
,求证:
 }的前n项和为
}的前n项和为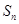 ,
,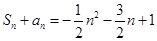 ,
,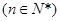 .
. ,证明:数列
,证明:数列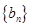 是等比数列;
是等比数列;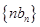 的前
的前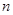 项和
项和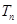 ;
;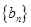 满足
满足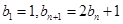 ,若数列
,若数列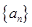 满足:
满足: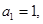 ,且当
,且当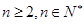 时,
时,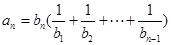
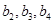 及
及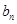 ;
; ,(注:
,(注: ).
).