Question

【题目】在正方体中，点、分别为、的中点，过点作平面使平面，平面若直线平面，则的值为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

作出图形，设平面分别交、于点、，连接、、，取的中点，连接、，连接交于点，推导出，由线面平行的性质定理可得出，可得出点为的中点，同理可得出点为的中点，结合中位线的性质可求得的值.

如下图所示：

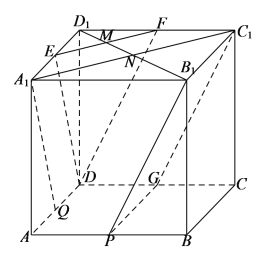
设平面分别交、于点、，连接、、，取的中点，连接、，连接交于点，

四边形为正方形，、分别为、的中点，则且，

四边形为平行四边形，且，

且，且，则四边形为平行四边形，

，平面，则存在直线平面，使得，

若平面，则平面，又平面，则平面，

此时，平面为平面，直线不可能与平面平行，

所以，平面，，平面，

平面，平面平面，，

，所以，四边形为平行四边形，可得，

为的中点，同理可证为的中点，，，因此，.

故选：B.