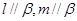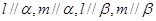题目内容
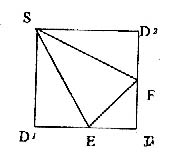
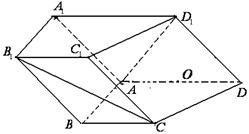
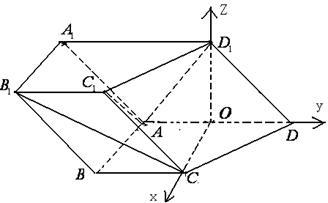
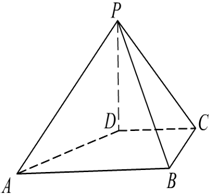
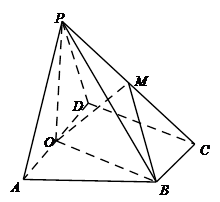
(本小题满分12分)如图,在四棱柱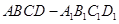 中,侧面
中,侧面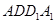 ⊥底面
⊥底面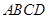 ,
, ,底面
,底面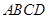 为直角梯形,其中
为直角梯形,其中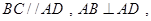
 ,O为
,O为 中点.
中点.
(Ⅰ)求证: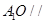 平面
平面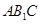 ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值.
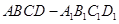 中,侧面
中,侧面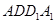 ⊥底面
⊥底面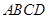 ,
, ,底面
,底面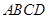 为直角梯形,其中
为直角梯形,其中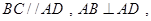
 ,O为
,O为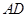 中点.
中点.
(Ⅰ)求证:
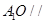 平面
平面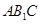 ;
;(Ⅱ)求锐二面角A—C1D1—C的余弦值.
(Ⅰ)证明:见解析;(Ⅱ)所求锐二面角A—C1D1—C的余弦值为 。
。
 。
。(I)证明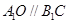 ,即证:四边形AB1CO为平行四边形.
,即证:四边形AB1CO为平行四边形.
(II)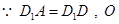 为
为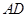 的中点,
的中点,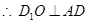 ,又侧面
,又侧面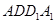 ⊥底面
⊥底面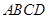 ,故
,故 ⊥底面
⊥底面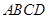 ,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
(Ⅰ)证明:如图,连接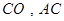 , …………..1分
, …………..1分
则四边形 为正方形, …………..2分
为正方形, …………..2分
 ,且
,且
故四边形 为平行四边形,…………..3分
为平行四边形,…………..3分
 , …………..4分
, …………..4分
又 平面
平面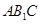 ,
,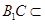 平面
平面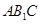 ……..5分
……..5分
 平面
平面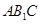 …………..6分
…………..6分
(Ⅱ)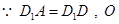 为
为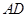 的中点,
的中点,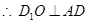 ,又侧面
,又侧面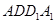 ⊥底面
⊥底面 ,故
,故 ⊥底面
⊥底面 ,…………..7分
,…………..7分
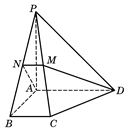
以 为原点,所
为原点,所 在直线分别为
在直线分别为 轴,
轴, 轴,
轴, 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则
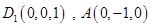 ,…………..8分
,…………..8分

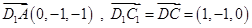 ,…………..9分
,…………..9分
设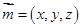 为平面
为平面 的一个法向量,由
的一个法向量,由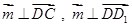 ,得
,得 ,
,
令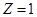 ,则
,则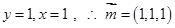 ………..10分
………..10分
又设 为平面
为平面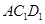 的一个法向量,由
的一个法向量,由 ,得
,得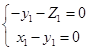 ,令
,令
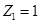 ,则
,则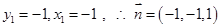 ,………..11分
,………..11分
则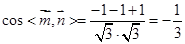 ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为 ………..12分
………..12分
注:第2问用几何法做的酌情给分.
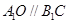 ,即证:四边形AB1CO为平行四边形.
,即证:四边形AB1CO为平行四边形.(II)
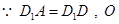 为
为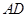 的中点,
的中点,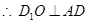 ,又侧面
,又侧面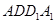 ⊥底面
⊥底面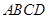 ,故
,故 ⊥底面
⊥底面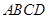 ,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.(Ⅰ)证明:如图,连接
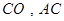 , …………..1分
, …………..1分则四边形
 为正方形, …………..2分
为正方形, …………..2分 ,且
,且
故四边形
 为平行四边形,…………..3分
为平行四边形,…………..3分 , …………..4分
, …………..4分又
 平面
平面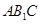 ,
,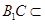 平面
平面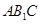 ……..5分
……..5分 平面
平面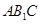 …………..6分
…………..6分(Ⅱ)
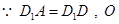 为
为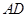 的中点,
的中点,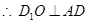 ,又侧面
,又侧面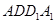 ⊥底面
⊥底面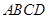 ,故
,故 ⊥底面
⊥底面 ,…………..7分
,…………..7分
以
 为原点,所
为原点,所 在直线分别为
在直线分别为 轴,
轴, 轴,
轴,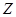 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则
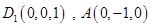 ,…………..8分
,…………..8分
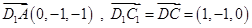 ,…………..9分
,…………..9分设
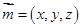 为平面
为平面 的一个法向量,由
的一个法向量,由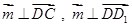 ,得
,得 ,
,令
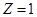 ,则
,则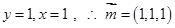 ………..10分
………..10分又设
 为平面
为平面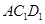 的一个法向量,由
的一个法向量,由 ,得
,得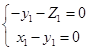 ,令
,令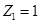 ,则
,则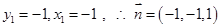 ,………..11分
,………..11分则
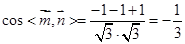 ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为 ………..12分
………..12分注:第2问用几何法做的酌情给分.

练习册系列答案
相关题目
 AD=1,CD=
AD=1,CD=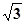 .
.
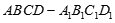 ,
,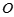 是底
是底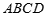 对角线的交点.
对角线的交点.
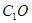 ∥面
∥面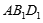 ;
;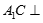 面
面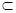 M,b
M,b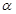 内的一条直线
内的一条直线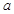 垂直与平面
垂直与平面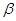 内的无数条直线,则
内的无数条直线,则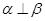
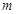 与平面
与平面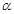 内的一条直线平行,则
内的一条直线平行,则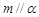
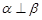 ,且
,且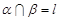 ,则过
,则过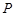 与
与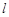 垂直的直线垂直于平面
垂直的直线垂直于平面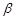
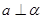 .
. 与平面
与平面 平行的是( )
平行的是( )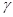
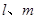 是
是