题目内容
8.(1)解不等式:|2x-2|<|x-4|;(2)记(1)中不等式的解集为A,当a,b∈A时,证明:2|a+b|<|4+ab|
分析 (1)不等式|2x-2|<|x-4|,即 (2x-2)2<(x-4)2,由此求得不等式的解集.
(2)由题意可得-2<a<2,-2<b<2,用比较法证得|4+ab|2-(2|a+b|)2>0,可得不等式 2|a+b|<|4+ab|成立.
解答 解:(1)不等式:|2x-2|<|x-4|,即 (2x-2)2<(x-4)2,即 3x2<12,
求得-2<x<2,故不等式的解集为(-2,2).
(2)记(1)中不等式的解集为A,当a,b∈A时,有-2<a<2,-2<b<2.
∵|4+ab|2-(2|a+b|)2=16+8ab+a2•b2-4(a2+2ab+b2)
=16+a2•b2-4a2-4b2=4(4-b2)+a2(b2-4)=(4-b2)(4-a2)>0,
∴|4+ab|>2|a+b|,即 不等式 2|a+b|<|4+ab|成立.
点评 本题考查绝对值函数,考查解不等式,考查不等式的证明,解题的关键是将不等式写成分段函数,利用作差法证明不等式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.直线$\left\{\begin{array}{l}x=1+2t\\ y=2+t\end{array}\right.$(t为参数)被圆x2+y2=4截得的弦长等于( )
| A. | $\frac{{2\sqrt{55}}}{5}$ | B. | $\frac{22}{5}$ | C. | $\frac{{2\sqrt{11}}}{5}$ | D. | $\frac{{22\sqrt{5}}}{5}$ |
20.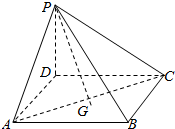 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )| A. | θ=$\frac{π}{4}$ | B. | cosθ=$\frac{2\sqrt{34}}{17}$ | C. | tanθ=$\frac{2\sqrt{2}}{3}$ | D. | sinθ=$\frac{\sqrt{3}}{3}$ |