题目内容
(1)已知a2+b2=1,求证:|a2+2ab-b2|≤
；(2)已知a、b、c是正实数,满足a+b+c=1,求证:a2+b2+c2≥
；
(3)已知a、b、c是三角形的三边,求证:
证明:根据问题的已知条件特征恰当换元.?
(1)由已知可设a=cosθ,b=sinθ,?
则|a2+2ab-b2|=|cos2θ+2cosθsinθ-sin2θ|?
=|cos2θ+sin2θ|=|sin(2θ+)|≤2.
(2)由已知可设a=+α,b=
+β,c=
+γ,
则α+β+γ=0.?
∴a2+b2+c2=(
+α)2+(
+β)2+(
+γ)2?
=
+
(α+β+γ)+α2+β2+γ2≥
.?
(3)设b+c-a=x,c+a-b=y,a+b-c=z,?
则x+y+z=a+b+c.?
由已知得x＞0,y＞0,z＞0,?
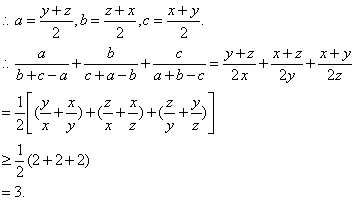
练习册系列答案
相关题目