题目内容
(本小题满分12分)
已知数列 的前
的前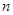 项和为
项和为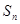 ,对一切正整数
,对一切正整数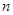 ,点
,点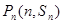 都在函数
都在函数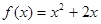 的图像上.
的图像上.
(Ⅰ)求数列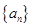 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的通项公式.
的通项公式.
(1)  (2)
(2) 
解析试题分析:解:
⑴由已知
∴n≥2时, ………………5分
………………5分
又 满足上式
满足上式
∴ ………………………………6分
………………………………6分
⑵由
∴ ……………………7分
……………………7分
∴

…… …………………………9分
…………………………9分
累加可得
∴ ……………………11分
……………………11分 满足上式
满足上式
∴ ………………………………12分
………………………………12分
考点:本试题考查了数列的通项公式的求解运用。
点评:解决该试题的关键是利用通项公式与前n项和的关系式来求解通项公式,同时还利用递推关系式,采用累加法 的思想来求解数列的通项公式,属于中档题,考查了同学们不同的角度来处理相应问题的能力运用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,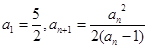
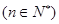 ,用数学归纳法证明:
,用数学归纳法证明: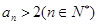 。
。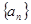 的通项公式为
的通项公式为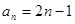 ,数列
,数列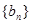 的前n项和为
的前n项和为 ,且满足
,且满足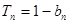
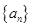 中是否存在使得
中是否存在使得 是
是 是公比
是公比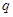 大于1的等比数列,
大于1的等比数列,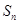 为数列
为数列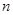 项和,已知
项和,已知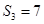 ,且
,且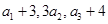 构成等差数列.
构成等差数列.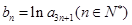 ,求数列
,求数列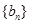 的前
的前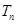 .
.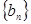 满足:
满足: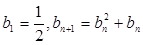 。
。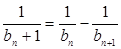 ;
;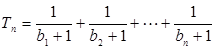 ,对任意的正整数
,对任意的正整数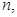
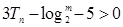 恒成立,求
恒成立,求 的取值范围。
的取值范围。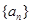 满足:
满足: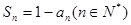 ,其中
,其中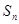 为
为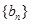 满足
满足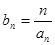 ,求
,求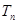 .
.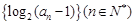 为等差数列,且
为等差数列,且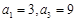
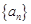 的通项公式;
的通项公式;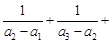 …
…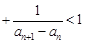 .
. 的前
的前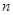 项和记为
项和记为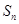 ,且满足
,且满足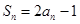 .
. ;
;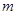 项的数列
项的数列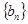 是连续的正整数数列,并且满足:
是连续的正整数数列,并且满足: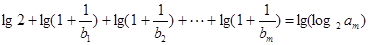 .
. 中,
中,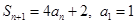 ;
;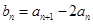 ,求证数列
,求证数列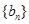 是等比数列;
是等比数列; ,求证:数列
,求证:数列 是等差数列;
是等差数列;