题目内容
【题目】已知函数![]() .
.
(1)求![]() 的极值点;
的极值点;
(2)若曲线 ![]() 上总存在不同两点
上总存在不同两点![]() ,使得曲线
,使得曲线![]() 在
在![]() 两点处的切线互相平行,证明:
两点处的切线互相平行,证明:![]()
【答案】(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)求函数的导数,并进行通分和因式分解的化简,并求得导数为0的![]() 值,
值,![]() 和
和![]() ,讨论两根的大小关系,并得到极值点两侧的单调性,判断是极大值还是极小值,(2)由题意可知
,讨论两根的大小关系,并得到极值点两侧的单调性,判断是极大值还是极小值,(2)由题意可知![]() ,并化简解得
,并化简解得![]() ,根据基本不等式
,根据基本不等式 ,化简为
,化简为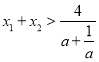 ,最后根据
,最后根据![]() ,证得不等式.
,证得不等式.
试题解析:(1)![]() 的定义域
的定义域![]() ,
,
 ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
∴![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点,
的极小值点,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,无极值点,
上单调递增,无极值点,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
∴![]() 是
是![]() 的极大值点,
的极大值点,![]() 是
是![]() 的极小值点;
的极小值点;
(2)由题知:![]() ,即:
,即:![]() ,
,
∴![]() ,
,
由于![]() ,且
,且![]() ,
,
∴![]() ,则有:
,则有:![]() ,
,
∴![]() ,
,
∴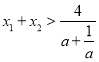 ,又
,又![]() ,
,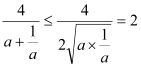 ,当且仅当
,当且仅当![]() 时取“=”,
时取“=”,
∴![]() ,即证.
,即证.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
【题目】在某省举办的娱乐节目“快乐向前冲”的海选过程中设置了几名导师,负责对每批初选合格的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在![]() 内的选手可以参加“待定”赛,如果通过,也可以参加第二轮比赛.
内的选手可以参加“待定”赛,如果通过,也可以参加第二轮比赛.

(1)已知成绩合格的200名参赛选手成绩的频率分布直方图如图,估计这200名参赛选手的成绩平均数和中位数;
(2)根据已有的经验,参加“待定”赛的选手能够进入第二轮比赛的概率如下表:
参赛选手成绩所在区间 |
|
|
每名选手能够进入第二轮的概率 |
|
|
假设每名选手能否通过“待定”赛相互独立,现有4名选手的成绩分别为(单位:分)43,45,52,58,记这4名选手在“待定”赛中通过的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.