题目内容
若F是椭圆
+
=1的右焦点，M是该椭圆上的点，A（-2，
）是该椭圆内一点，则|MA|+2|MF|的最小值是（ ）
| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
A、8+
| ||
B、4+
| ||
| C、10 | ||
| D、8 |
分析：先根据椭圆方程求得椭圆的离心率和右准线方程，进而作M垂直于椭圆的右准线交准线于N，根据椭圆定义可知2|MF|=|MN|，|MA|+2|MF|的最小值是即是求|MA|+|MN|的最小值，很明显当M，A，N三点共线的时候取最小值．
解答：解：依题意可知a=4，b=2
，
∴c=
=2
∴e=
=
，右准线方程为x=8
作M垂直于椭圆的右准线交准线于N，根据椭圆第二定义可知2|MF|=|MN|
∴|MA|+2|MF|=|MA|+|MN|，很明显当M，A，N三点共线的时候取最小值，
此时点A到右准线距离为2+8=10
故选C
| 3 |
∴c=
| 16-12 |
∴e=
| c |
| a |
| 1 |
| 2 |
作M垂直于椭圆的右准线交准线于N，根据椭圆第二定义可知2|MF|=|MN|
∴|MA|+2|MF|=|MA|+|MN|，很明显当M，A，N三点共线的时候取最小值，
此时点A到右准线距离为2+8=10
故选C
点评：本题主要考查了椭圆的应用．解题的关键是利用椭圆的第二定义．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
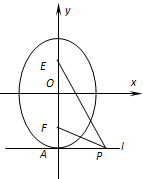（1）已知平面上两定点A（-2，0）．B（2，0），且动点M标满足