题目内容
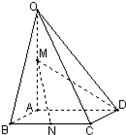
如图,在四棱锥O—ABCD中,底面ABCD是菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:
![]() ⑴平面BDO⊥平面ACO;
⑴平面BDO⊥平面ACO;![]() ⑵直线EF∥平面OCD.
⑵直线EF∥平面OCD.
(1)略 ![]() (2)略
(2)略
解析:
证:⑴∵底面ABCD是菱形,∴AC⊥BD,又∵OA⊥面ABCD,∴OA⊥BD
∴BD⊥面OAC,∴平面BDO⊥面OAC
⑵取OD的中点G,连结GC,∵E为OA中点, F为BC中点![]()
![]()
![]() 又∵FC
又∵FC ![]() AD,∴GC FC,∴四边形EFCG为平行四边形,
AD,∴GC FC,∴四边形EFCG为平行四边形,
∴EF∥GC,GD![]() 平面ODC,EF
平面ODC,EF![]() 平面ODC,∴EF∥平面OCD.
平面ODC,∴EF∥平面OCD.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
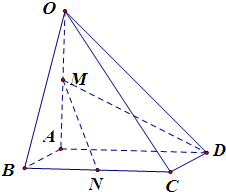 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题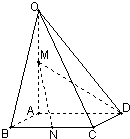 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC= 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形, 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,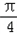 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.