题目内容
已知△ABC的两边长分别为AB=25，AC=39，且O为△ABC外接圆的圆心．（注：39=3×13，65=5×13）
（1）若外接圆O的半径为
，且角B为钝角，求BC边的长；
（2）求
•
的值．
（1）若外接圆O的半径为
| 65 |
| 2 |
（2）求
| AO |
| BC |
（1）由正弦定理有
=
=2R（R为外接圆半径），
∴
=
=65，
∴sinB=
，sinC=
，又B为钝角，
∴cosC=
，cosB=-
，
∴sin（B+C）=sinBcosC+cosBsinC=
×
+
×（-
）=
，
又
=2R，∴BC=2RsinA=65sin（B+C）=16；
（2）由已知得：
+
=
，∴（
+
）2=
2，
即|
|2+2
•
+|
|2=|
|2=392，
同理
+
=
，∴|
|2+2
•
+|
|2=|
|2=252，
两式相减得：2
•
-2
•
=（39+25）（39-25）=896，
即2
•
=896，
则
•
=448．
| AB |
| sinC |
| AC |
| sinB |
∴
| 25 |
| sinC |
| 39 |
| sinB |
∴sinB=
| 3 |
| 5 |
| 5 |
| 13 |
∴cosC=
| 12 |
| 13 |
| 4 |
| 5 |
∴sin（B+C）=sinBcosC+cosBsinC=
| 3 |
| 5 |
| 12 |
| 13 |
| 5 |
| 13 |
| 4 |
| 5 |
| 16 |
| 65 |
又
| BC |
| sinA |
（2）由已知得：
| AO |
| OC |
| AC |
| AO |
| OC |
| AC |
即|
| AO |
| AO |
| OC |
| OC |
| AC |
同理
| AO |
| OB |
| AB |
| AO |
| AO |
| OB |
| OB |
| AB |
两式相减得：2
| AO |
| OC |
| AO |
| OB |
即2
| AO |
| BC |
则
| AO |
| BC |
练习册系列答案
名校课堂系列答案
相关题目
已知△ABC的两边长分别为AB=25，AC=39，且O为△ABC外接圆的圆心．（注：39=3×13，65=5×13）
（1）若外接圆O的半径为
，且角B为钝角，求BC边的长；
（2）求
•
的值．
（1）若外接圆O的半径为
| 65 |
| 2 |
（2）求
| AO |
| BC |
,则其外接圆半径为_____________.
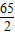，且角B为钝角，求BC边的长；
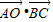的值．
，且角B为钝角，求BC边的长；
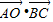的值．