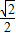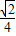题目内容
如图所示，已知空间四边形ABCD，E、F分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且
，求证直线EF、GH、AC交于一点．
同解析。
解析:
如答图所示，∵AE＝EB，AH＝HD，∴EH//BD，且EH＝
BD，
∵
，∴FG//BD，且FG＝
BD，
∴EH//FG，且EH≠FG，
故四边形EFGH为梯形，则EF与GH必相交，
设交点为P，P∈平面ABC，又P∈平面DAC，
又平面BAC∩平面DAC＝AC，故P∈AC，
即EF、GH、AC交于一点.
练习册系列答案
相关题目
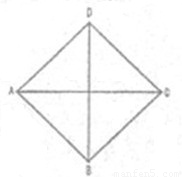
我们将底面是正方形，侧棱长都相等的棱锥称为正四棱锥．已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同，且如图所示，视图中四边形ABCD是边长为1的正方形，则该几何体的体积为（ ）
.
.
的底面ABCD为正方形，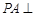
平面ABCD，E、F分别是BC，PC的中点，
，
．
平面
；
的大小．
，，
，则
，
，
