题目内容
4.已知一个实心铁质的几何体的正视图和侧视图是全等的正三角形,俯视图是半径为3的圆,将3个这样的几何体熔成一个实心正方体,则正方体的表面积为( )| A. | 54$\root{3}{3{π}^{2}}$ | B. | 54$\root{3}{3π}$ | C. | 54$\root{3}{12{π}^{2}}$ | D. | 54$\root{3}{12π}$ |
分析 几何体为圆锥,底面半径为3,利用体积相等求出正方体的棱长,得出表面积.
解答 解:∵实心铁质的几何体的正视图和侧视图是全等的正三角形,俯视图是半径为3的圆,
∴铁质几何体为轴截面为正三角形的圆锥,底面半径r=3,
∴圆锥的高h=3$\sqrt{3}$.
设正方体棱长为a,则a3=3×$\frac{1}{3}π{r}^{2}h$=27$\sqrt{3}π$,
∴a=3$\root{3}{\sqrt{3}π}$,
∴正方体的表面积S=6a2=54$\root{3}{3{π}^{2}}$.
故选:A.
点评 本题考查了圆锥的三视图,结构特征,和体积计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,且斜率为2的直线l与双曲线的相交于点A,B,若弦AB的中点横坐标取值范围为(2c,4c),则该双曲线的离心率的取值范围是( )
| A. | (3,4) | B. | (2,3) | C. | $(\sqrt{3},4)$ | D. | $(\sqrt{3},2)$ |
9.已知x,y满足约束条件$\left\{\begin{array}{l}x≥1\\ y≥-1\\ 4x+y≤9\\ x+y≤3\end{array}\right.$,若目标函数z=mx+y(m>0)的最大值为1,则m的值是( )
| A. | $-\frac{20}{9}$ | B. | 1 | C. | 2 | D. | 5 |
16.将4本完全相同的小说,1本诗集全部分给4名同学,每名同学至少1本书,则不同分法有( )
| A. | 24种 | B. | 28种 | C. | 32种 | D. | 16种 |
13.执行如图所示的程序框图,若输出的S的值为$\frac{5}{2}$,则实数k的取值范围为( )
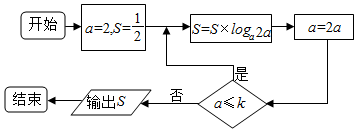

| A. | [16,64] | B. | [16,32) | C. | [32,64) | D. | (32,64) |