题目内容
6.已知数列{an}满足a1=1,an=$\frac{{2{S_n}^2}}{{2{S_n}-1}}$(n≥2),其中Sn为{an}的前n项和,则S2016=$\frac{1}{4031}$.分析 通过对an=$\frac{{2{S_n}^2}}{{2{S_n}-1}}$(n≥2)变形可知2SnSn-1=Sn-1-Sn,进而可知数列{$\frac{1}{{S}_{n}}$}是首项为1、公差为2的等差数列,计算即得结论.
解答 解:∵an=$\frac{{2{S_n}^2}}{{2{S_n}-1}}$(n≥2),
∴2${{S}_{n}}^{2}$=2Snan-an,
∴2${{S}_{n}}^{2}$-2Snan=Sn-1-Sn,即2SnSn-1=Sn-1-Sn,
∴2=$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$,
又∵$\frac{1}{{S}_{1}}$=1,
∴数列{$\frac{1}{{S}_{n}}$}是首项为1、公差为2的等差数列,
∴S2016=$\frac{1}{1+2(2016-1)}$=$\frac{1}{4031}$,
故答案为:$\frac{1}{4031}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.600°角是第( )象限的角.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
18.设三棱锥O-ABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,G是△ABC的重心,则$\overrightarrow{OG}$等于( )
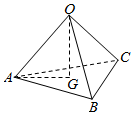

| A. | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$) | D. | $\frac{1}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$) |
15.已知函数f(x)=sinx-cosx且f′(x)=2f(x),则tanx=( )
| A. | -3 | B. | 3 | C. | 1 | D. | -1 |
16.命题“?x∈R,都有log2x>0成立”的否定为( )
| A. | ?x0∈R,使log2x0≤0成立 | B. | ?x0∈R,使log2x>0成立 | ||
| C. | ?x∈R,都有log2x≥0成立 | D. | ?x∈R,都有log2x>0成立 |
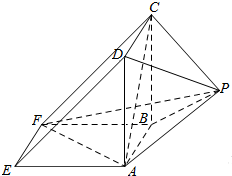 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.